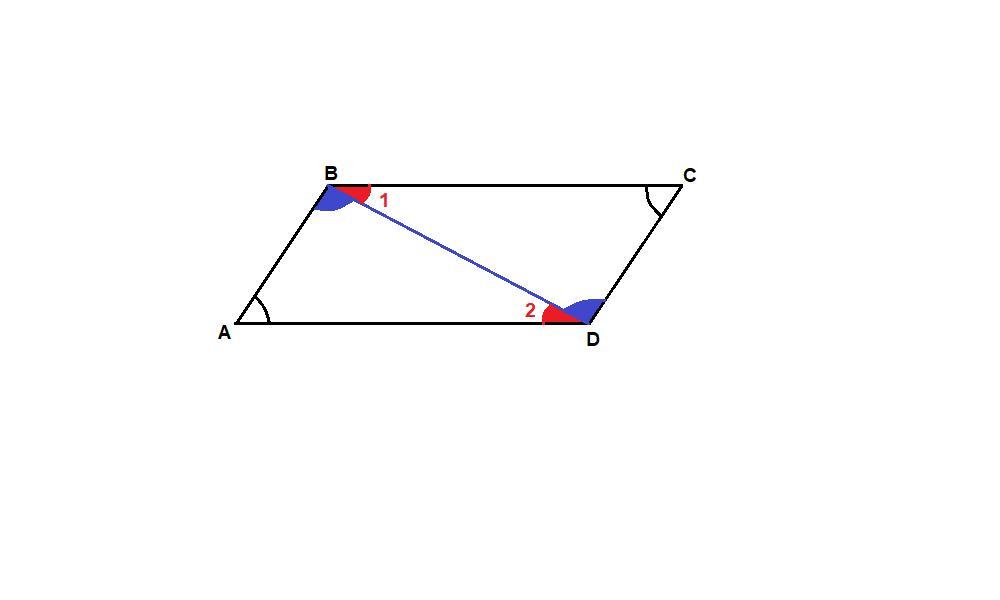
В четырехугольнике ABCD : AB||CD , угол A=C.Доказать что ABCD-параллелограмм
Ответы
Пусть ABCD – данный четырехугольник. По условию AB\CD мы вполне можем провести 2 диоганали так что у нас выидет AO = OC , BO = OD . Так как углы ( AOB ) и ( COD ) равны как вертикальные, то по теореме 4.1 треугольник AOB равен треугольнику COD , и, следовательно, углы ( OAB ) и ( OCD ) равны. Эти углы являются внутренними накрест лежащими при прямых ( AB ) и ( CD ) и секущей ( AC ) и по теореме 3.2 прямые ( AB ) и ( CD ) параллельны. Аналогично из равенства треугольников AOD и COB следует равенство углов ( OAD ) и ( OCB ) и по теореме 3.2 – параллельность прямых ( AD ) и ( BC ). Из полученных результатов следует, что четырехугольник ABCD – параллелограмм. Теорема доказана.
Доказательство:
∠AВD = ∠CDB как накрест лежащие углы при пересечении параллельных прямых АВ и CD секущей BD.
Сумма углов треугольника равна 180°.
ΔABD: ∠2 = 180° - (∠А + ∠ABD)
ΔCDB: ∠1 = 180° - (∠C + ∠CDB)
Так как ∠А = ∠С по условию и ∠AВD = ∠CDB, то
∠1 = ∠2, а эти углы - накрест лежащие при пересечении прямых ВС и AD секущей BD, значит
ВС ║ AD.
Значит ABCD - параллелограмм по определению (параллелограмм - это четырехугольник, у которого противоположные стороны параллельны).