Question

Площадь прямоугольного треугольника равна 242√3. Один из острых углов равен 60∘. Найдите длину катета, прилежащего к этому углу.

Answer 1

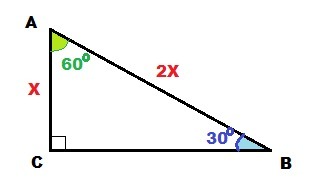
ΔABC - прямоугольный : ∠C = 90°; ∠A = 60°; S = 242√3

Найти длину катета АС

По свойству острых углов прямоугольного треугольника

∠B = 90° - ∠A = 90° - 60° = 30°

Катет АС лежит против угла 30° ⇒ равен половине гипотенузы АВ ⇒

АВ = 2 АС

Площадь треугольника можно вычислить по формуле

$S_{ABC}=dfrac{AC*AB*sinA}{2}= \ \ =dfrac{AC*2AC*sin60^o}{2}=dfrac{2AC^2*frac{sqrt{3}}{2}}{2} =dfrac{sqrt{3}}{2}AC^2$

По условию

$S_{ABC} =dfrac{sqrt{3}}{2}AC^2=242sqrt{3} \ \ AC^2 = 242*2 \ AC = sqrt{484} = 22$

Ответ: длина катета равна 22