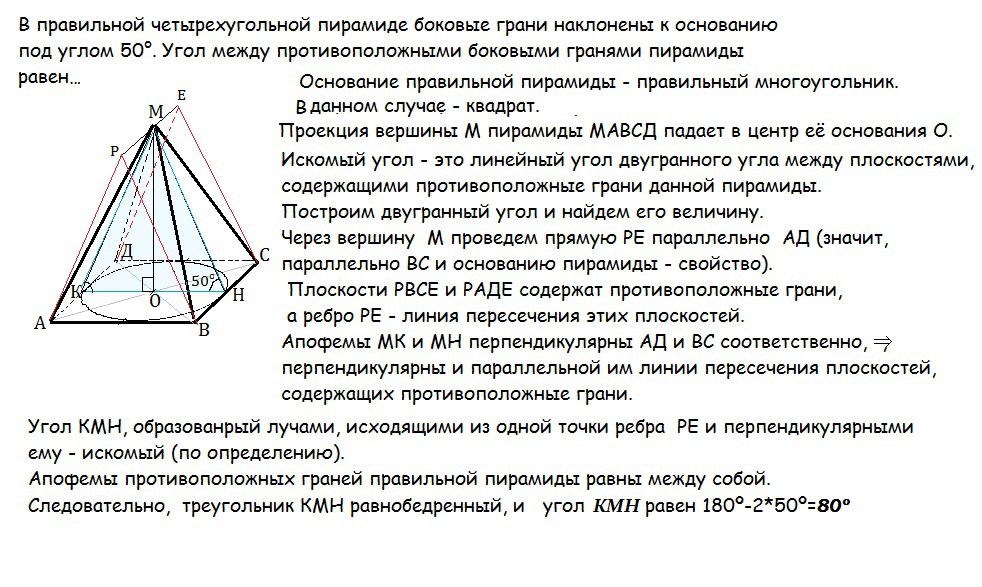
В правильной четырехугольной пирамиде боковые грани наклонены к основанию под углом 50°. Угол между противоположными боковыми гранями пирамиды равен…
Ответы
<SFO=<SHO=50
<FSO=<HSJ=90-50=40
<FSH=2<DSO=2*40=80
Основание правильной четырехугольной пирамиды - квадрат.
Проекция вершины пирамиды падает в центр её основания.
Пусть данная пирамида МАВСД.
О - точка пересечения диагоналей основания и является его центром .
Искомый угол - это линейный угол двугранного угла между плоскостями, содержащими противоположные грани данной пирамиды.
Двугранный угол измеряется величиной своего линейного угла.
Чтобы ответить на вопрос задачи, нужно построить нужный линейный угол и найти его величину..
Через вершину пирамиды М проведем прямую РЕ || АД и, значит, параллельно ВС и основанию пирамиды - свойство). Плоскости РВСЕ и РАДЕ содержат противоположные грани и РЕ - линия их пересечения.
Апофемы МК и МН, являясь высотами боковых граней, перпендикулярны АД и ВС соответственно, ⇒, перпендикулярны и РЕ - параллельной им линии пересечения плоскостей, содержащих грани.
Угол КМН, образованный лучами, исходящими из одной точки линии пересечения РЕ и перпендикулярными ей - искомый по определению.
Апофемы противоположных граней правильной пирамиды равны между собой.
Следовательно, треугольник КМН равнобедренный, и угол КМН равен 180º-2*50º=80º