Предмет: Алгебра,
автор: weit
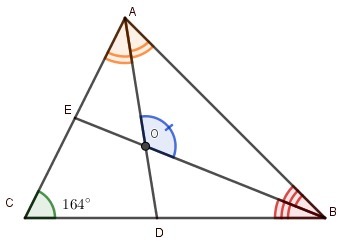
В треугольнике ABC угол C равен 164 градуса, AD и BE —
биссектрисы, пересекающиеся в точке O. Найдите
угол AOB.
Ответы
Автор ответа:
0
Ответ: 172°.
Пошаговое объяснение:
Сумма внутренних углов треугольника равна 180°, то есть
∠ABC + ∠ACB + ∠BAC = 180°
∠ABC + ∠BAC = 180° - ∠ACB = 180° - 164° = 16°
Так как AD и BE — биссектрисы углов ABC и BAC соответственно, то
∠ABC + ∠BAC = 2∠OAB + 2∠OBA
∠OAB + ∠OBA = (∠ABC + ∠BAC) : 2 = 16° : 2 = 8°
Тогда из треугольника AOB: ∠AOB + ∠OBA + ∠OAB = 180°
∠AOB = 180° - (∠OBA + ∠OAB) = 180° - 8° = 172°
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Алгебра,
автор: bajgudeevr
Предмет: Алгебра,
автор: sezimborisova98
Предмет: Литература,
автор: Аноним
Предмет: Математика,
автор: absoluteweirdo