Предмет: Алгебра,
автор: kittycat13
Найдите наименьшее значение параметра а, при котором уравнение(смотри во вложениях) имеет положительный корень.
Буква "р" в уравнении это пи.
Приложения:
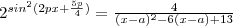
Ответы
Автор ответа:
0
Рассмотрим отдельные функций , видно что у функций слева максимальное и минимальное значений соответственно будут равны 1 и 2
У функций максимальное значение равна 1.
максимальное значение равна 1.
Откуда видно что они могут пересекаться только в точке равным 1

Тогда уравнение в правой части будет

то есть при
У функций
Откуда видно что они могут пересекаться только в точке равным 1
Тогда уравнение в правой части будет
то есть при
Похожие вопросы
Предмет: Химия,
автор: nuraikaasanova06
Предмет: Английский язык,
автор: sukharevserzh
Предмет: Обществознание,
автор: Аноним
Предмет: Химия,
автор: Fed2013
Предмет: Литература,
автор: Аноним