Question

помогите пожалуйста.
с решением, конечно же

Answer 1

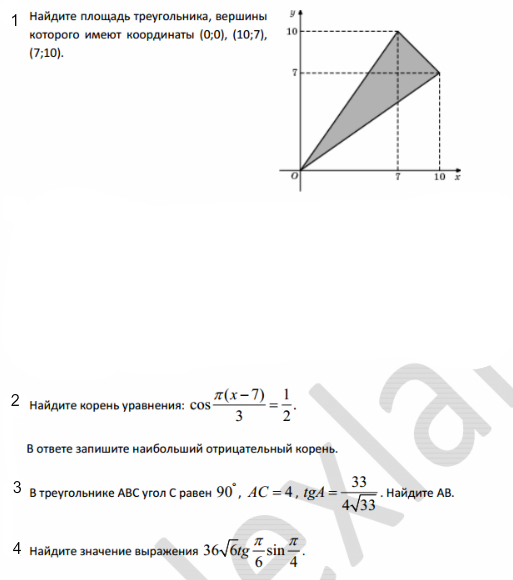
1. А(0;0), В(10;7), С(7;10) - треугольник. Найдём длины его сторон.
$AB=sqrt{(10-0)^2+(7-0)^2}=sqrt{100+49}=sqrt{149}\AC=sqrt{(7-0)^2+(10-0)^2}=sqrt{49+100}=sqrt{149}\BC=sqrt{(7-10)^2+(10-7)^2}=sqrt{9+9}=sqrt{18}=3sqrt2$
AB=BC, значит треугольник равнобедренный. Его площадь равна половине произведения основания и высоты. Высота AD делит сторону BC пополам. Найдём координаты точки D, как середины отрезка
$Dleft(frac{7+10}2;frac{10+7}2right)=(8,5;;8,5)$
Найдём длину высоты AD
$AD=sqrt{(8,5-0)^2+(8,5-0)^2}=sqrt{2cdot8,5^2}=8,2sqrt2$
Площадь ABC
$S=frac12cdot3sqrt2cdot8,5sqrt2=frac12cdot3cdot8,5cdot2=25,5$ кв.ед.
$2.;cosfrac{pi(x-7)}3=frac12\frac{pi(x-7)}3=fracpi3+2pi n,;ninmathbb{Z}\fracpi3(x-7)=fracpi3+2pi n\x-7=1+6n\x=8+6n\8+6n<0\6n<-8\n<-1frac13\ninmathbb{Z}Rightarrow nleq-2\x=8+6cdot(-2)=8-12=-4$
$3.;frac{33}{4sqrt{33}}=frac{sqrt{33}cdotsqrt{33}}{4sqrt{33}}=frac{sqrt{33}}4\tgA=frac{BC}{AC}\frac{sqrt{33}}{4}=frac{BC}{4}\BC=sqrt{33}\AB=sqrt{BC^2+AC^2}=sqrt{33+frac{33}{16}}=sqrt{frac{528+33}{16}}=frac{sqrt{561}}{4}\4.;36sqrt6tgfracpi6sinfracpi4=36sqrt6cdotfrac1{sqrt3}cdotfrac1{sqrt2}=frac{36sqrt6}{sqrt6}=36$