Question

Постройте график функции y=x^2−4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.

Answer 1

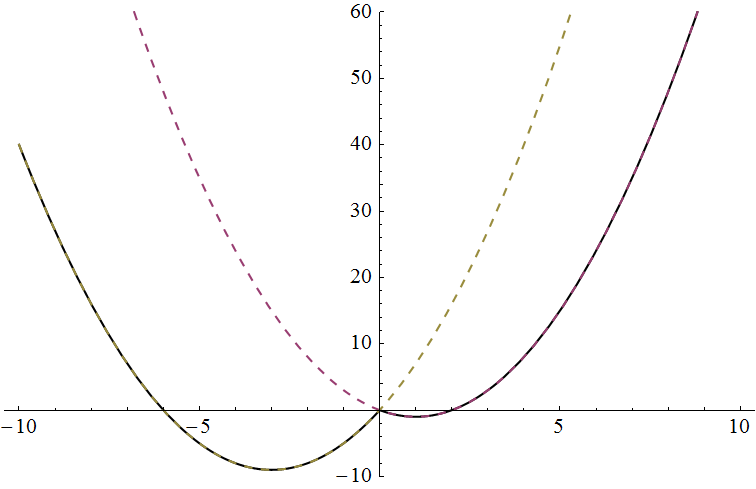
График склеен из двух парабол: x^2-2x при x>=0 и x^2+6x при x<0.

Найдём вершины:
x^2 - 2x = (x^2 - 2x + 1) - 1 = (x - 1)^2 - 1     вершина в (1, -1)
x^2 + 6x = (x^2 + 6x + 9) - 9 = (x + 3)^2 - 9   вершина в (-3, -9)

при c < -9 решений нет
при c = -9 одно решение
при -9 < c < -1 два решения
при c = -1 три решения
при -1 < c < 0 четыре решения
при c = 0 три решения
при c > 0 два решения