Предмет: Алгебра,
автор: valik1171
Найти все пары чисел (p, q) чтобы многочлен (картинка) разлагался в произведение многочленов с целыми коэффициентами
Приложения:
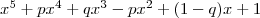
Ответы
Автор ответа:
0
Для начало если коэффициенты целые , то следует что если мы представим многочлен в виде произведение данных многочленов  , то число
, то число  должен быть натуральным делителем , возможен вариант
должен быть натуральным делителем , возможен вариант  что при подстановки отпадает.
что при подстановки отпадает.
Рассмотрим вариант

Из данного выражение следует следствия

то есть единственный вариант когда

То есть
Рассмотрим вариант
Из данного выражение следует следствия
то есть единственный вариант когда
То есть
Похожие вопросы
Предмет: Русский язык,
автор: olesia71
Предмет: Русский язык,
автор: EGORXZ19
Предмет: Русский язык,
автор: Holiday83
Предмет: Информатика,
автор: leikajaguar
Предмет: Математика,
автор: MACHINES