Question

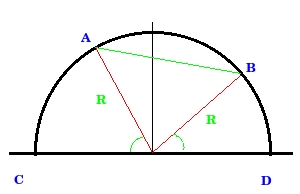
На полуокружности CD взяты точки А и В так,что дуга АС=65 градусов,дуга ВD=55 градусов. Найдите хорду АВ,если радиус окружности равен 10 см.

Answer 1

Дуга АВ = 180 - 65-55 = 60°. И 2 остальных тоже равны по 60° ((180-60) / 2 = 60). Значит, хорда АВ - это сторона равностороннего треугольника. АВ = R = 10 см.

Answer 2

Можно задачку решить ни чего не считая, только рассуждая.
У нас есть полуокужность, A и B точки отмеченые на ней, если соединить А и B c серединой отрезка CD точкой О плучим три угла
COA =  65
BOD = 55
AOB = 180 - 65 - 55 =60
Отрезки AO BO AB образуют треугольник у кторого как минимум две стороны равны (АО и ВО) и один угол 60 градусов следовательно это равнобедренный треугольник у которого один угол 60 градусов. В треугольнике сумма всех углов 180 градусов значит оставшиеся одинаковые углы равны (180 - 60)/2 = 60.
Имеем тругольник равносторонний следовадельно сторона АB, которая является хордой, равна 10 см.