Предмет: Алгебра,
автор: русская25
значения:
а = 1
b = -1
с = 3
m = -2
n= -3
Приложения:

Ответы
Автор ответа:
0
(1) подставляем значения, и получаем y=
-----
1) Ищем ОДЗ
2x+3≠0
x≠-3/2
x∈(-∞;-3/2)U(-3/2;∞)
---------
2) ищем вертикальные асимптоты
 ∞
∞
 ∞
∞
значит, прямая х=-3/2 - вертикальная асимптота.
----------
3) проверим функцию на четность и нечетность
а) четность
f(x)=f(-x)
 ≠
≠
функция не является четной.
б) на нечетность
f(x)=-f(x)
 ≠-(
≠-( )
)
функция не является нечетной.
----------
4) промежутки убывания и возрастания
ищем производную, приравняем к нулю и найдем критические точки функции
f '(x)=( )'=(4х²+12х+15)/(2x+3)²=0
)'=(4х²+12х+15)/(2x+3)²=0
x=-3/2
берем пробные точки и проверяем знак
f '(-2)=7 (+)
f '(0)=15/9 (+)
значит, функция при всех Х возрастает.
-----------
5) периодичность.
видно, что
f(x)≠f(x+T)
----------
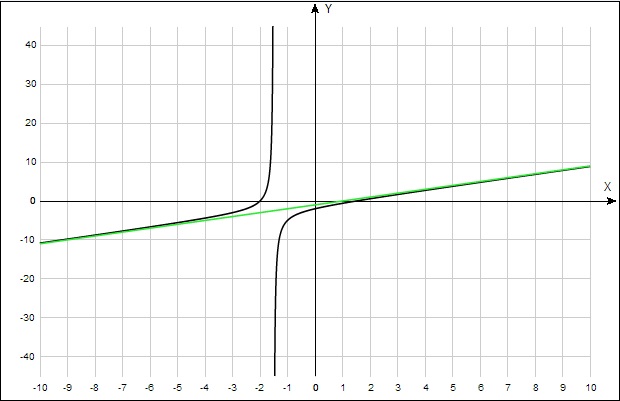
6) там есть наклонная асимптота, но я не знаю как ее найти.
график
-----
1) Ищем ОДЗ
2x+3≠0
x≠-3/2
x∈(-∞;-3/2)U(-3/2;∞)
---------
2) ищем вертикальные асимптоты
значит, прямая х=-3/2 - вертикальная асимптота.
----------
3) проверим функцию на четность и нечетность
а) четность
f(x)=f(-x)
функция не является четной.
б) на нечетность
f(x)=-f(x)
функция не является нечетной.
----------
4) промежутки убывания и возрастания
ищем производную, приравняем к нулю и найдем критические точки функции
f '(x)=(
x=-3/2
берем пробные точки и проверяем знак
f '(-2)=7 (+)
f '(0)=15/9 (+)
значит, функция при всех Х возрастает.
-----------
5) периодичность.
видно, что
f(x)≠f(x+T)
----------
6) там есть наклонная асимптота, но я не знаю как ее найти.
график
Приложения:
Автор ответа:
0
спасибо огромное!
Автор ответа:
0
Смотри ответ во вложении
Приложения:


Автор ответа:
0
Спасибо огромное за помощь!
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: guccicat46
Предмет: Другие предметы,
автор: Аноним
Предмет: Химия,
автор: ьегемот85
Предмет: Обществознание,
автор: Fenichka666