Question

Дан ромб со стороной 32,6 см и углом 48*. Из вершины острого угла к плоскости ромба восставлен перпендикуляр длиной 56,3 см. Найти расстояние от вершины перпендикуляра до точки пересечния диагоналей ромба.

Answer 1

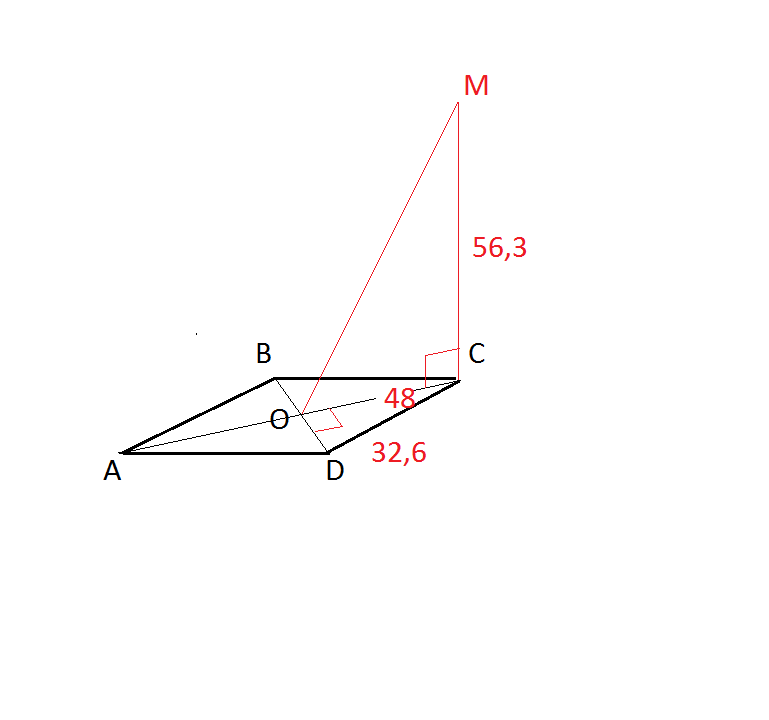
сделаем построение по условию
искомое расстояние  ОМ
сторона ромба  DC = 32,6 см
диагонали ромба пересекаются под углом 90 град
ODC - прямоугольный
< ОСD = 1/2 <BCD = 1/2 48 = 24 град
ОС = DC*cos24 = 32,6*cos24
MC перпендикуляр к плоскости ромба
АС лежит плоскости ромба, значит  МС перпендикулярна ОС
ОС - проекция наклонной МО на плоскость ромба
три точки ОСМ образуют плоскость ОСМ
треугольник ОСМ прямоугольный
по формуле Пифагора  
OM^2 = OC^2 +MC^2
OM = √ ОС^2 +MC^2 = √ ( (32,6*cos24)^2 + 56.3^2 ) = 63,7 см

ответ 63,7 см

Answer 2

там наверное в ответе ошибка не 32,6^2, а 56,3^2, а то получается что катет больше гипотенузы