Предмет: Геометрия,
автор: veronuka647
в трапеции ABCD основания AB и CD равны 3 и 7 соответственно , а углы при основании AB равны 33 и 57 градусов. найдите длину отрезка MN, где M и N - середины оснований AB и CD.
Ответы
Автор ответа:
0
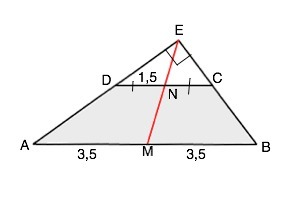
Так как по условию углы при АВ острые, АВ - большее основание. М и N середины АВ и CD, ⇒ АМ=МВ и СN=ND. Продлив боковые стороны трапеции до пересечения в т.Е, получим треугольник с углом Е=180°-33°-57°=90° ⇒ ∆ АВЕ - прямоугольный, АВ - его гипотенуза, ЕМ - медиана. По свойству медианы прямоугольного треугольника ЕМ=АВ:2=3,5 ЕN- медиана прямоугольного ∆ CED, EN=CD:2=1,5 ⇒ МN=3,5 -1,5=2 (ед. длины)
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: 710samsung77758
Предмет: Русский язык,
автор: merash19
Предмет: Алгебра,
автор: Аноним