Question

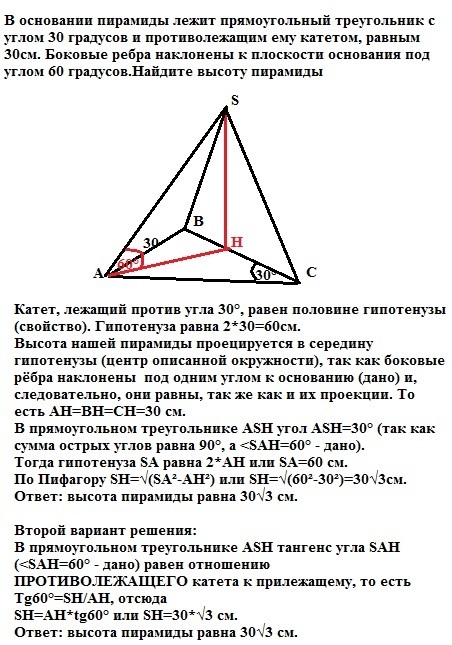
В основании пирамиды лежит прямоугольный треугольник с углом 30 градусов и противолежащим ему катетом, равным 30см. Боковые ребра наклонены к плоскости основания под углом 60 градусов.Найдите высоту пирамиды

Answer 1

Катет, лежащий против угла 30°, равен половине гипотенузы (свойство). Гипотенуза равна 2*30=60см.
Высота нашей пирамиды проецируется в середину гипотенузы (центр описанной окружности), так как боковые рёбра наклонены  под одним углом к основанию (дано) и, следовательно, они равны, так же как и их проекции. То есть АН=ВН=СН=30 см.
В прямоугольном треугольнике ASH угол АSH=30° (так как сумма острых углов равна 90°, а <SAH=60° - дано).
Тогда гипотенуза SA равна 2*АН или SA=60 см.
По Пифагору SH=√(SA²-AH²) или SH=√(60²-30²)=30√3см.
Ответ: высота пирамиды равна 30√3 см.

Второй вариант решения:
В прямоугольном треугольнике ASH тангенс угла SAH
(<SAH=60° - дано) равен отношению ПРОТИВОЛЕЖАЩЕГО катета к прилежащему, то есть Tg60°=SH/AH, отсюда
SH=AH*tg60° или SH=30*√3 см.
Ответ: высота пирамиды равна 30√3 см.