Предмет: Геометрия,
автор: irina2587
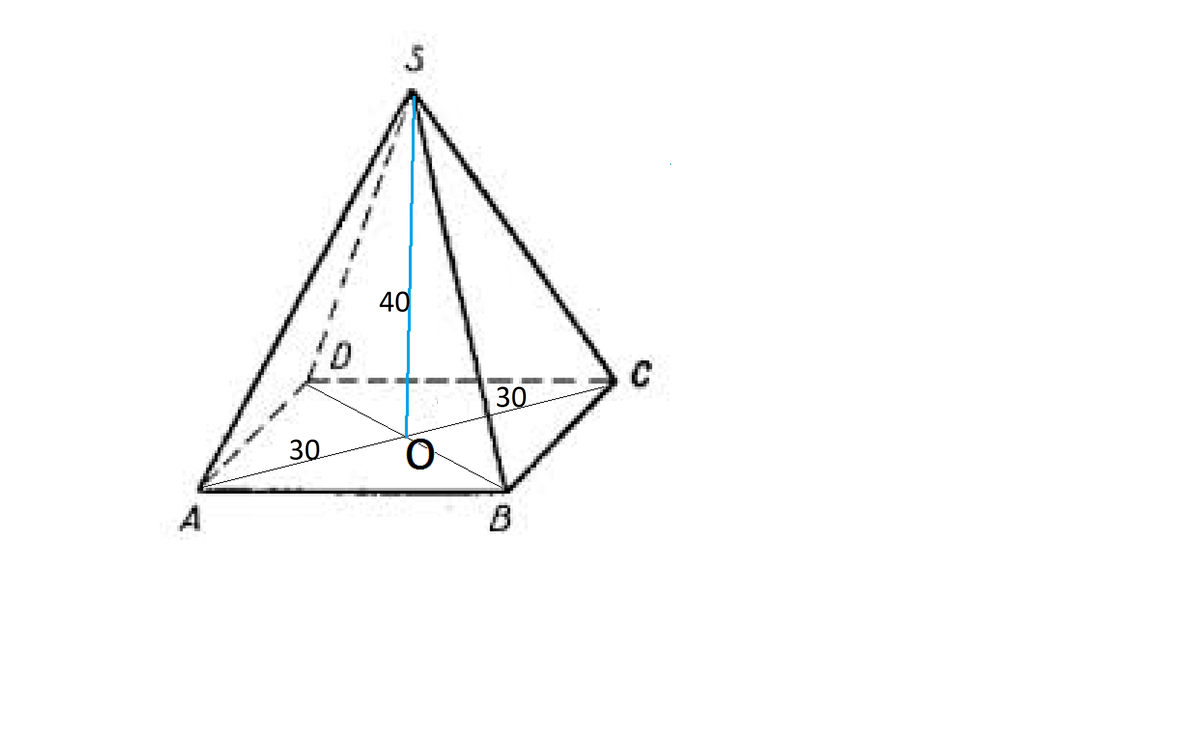
В правильной четырёхугольной пирамиде точка О центр основания, S вершина, SO=40 Ac=60.найдите боковое ребро SA.
Ответы
Автор ответа:
0
Основание правильной четырехугольной пирамиды - квадрат.
Основание её высоты - центр основания, и это точка пересечения равных диагоналей, которая делит их пополам.
Следовательно,
ОА=60:2=30
Высота пирамиды перпендикулярна ее основанию.
Отношение катетов прямоугольного треугольника SOA = 3:4, и это отношение катетов египетского треугольника.
Отсюда следует, что АО:SO:SA=3:4:5
коэффициент подобия
30:3=10
SA=5*10=50.
Проверим по т. Пифагора:
SA=√(30²+40²)=√2500=50
Ответ:SA=50
-------
[email protected]
Основание её высоты - центр основания, и это точка пересечения равных диагоналей, которая делит их пополам.
Следовательно,
ОА=60:2=30
Высота пирамиды перпендикулярна ее основанию.
Отношение катетов прямоугольного треугольника SOA = 3:4, и это отношение катетов египетского треугольника.
Отсюда следует, что АО:SO:SA=3:4:5
коэффициент подобия
30:3=10
SA=5*10=50.
Проверим по т. Пифагора:
SA=√(30²+40²)=√2500=50
Ответ:SA=50
-------
[email protected]
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: nshepelyuk3
Предмет: Обществознание,
автор: timapalamarchuk00
Предмет: Английский язык,
автор: adelakubatbekova
Предмет: Химия,
автор: zinya2012