Предмет: Математика,
автор: Trelia
Расставить пределы интегрирования в повторном интеграле для двойного интеграла и изменить порядок интегрирования
Приложения:
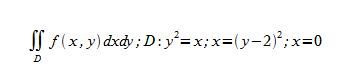
Ответы
Автор ответа:
0
Получили
Переопределяем множество:
Интеграл на множество:
Похожие вопросы