Предмет: Геометрия,
автор: Anzhela96
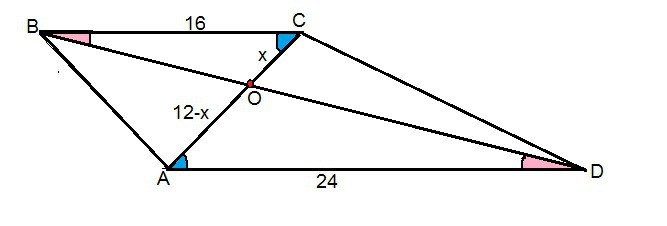
в трапеции АВСД с основаниями АД и ВС диагонали пересекаются в точке О.АД=24см,ВС=16см,АС=12см.Найдите длину отрезков ОА и ОС.
Ответы
Автор ответа:
0
Диагонали АС и ВD пересекаются в точке О и с основаниями образую треугольники ВОС и АОD.
Примем ОС=х, тогда АО=12-х
Накрестлежащие углы в этих треугольниках равны⇒
∆ АОD ~ ∆ ВОС по двум равным углам при основаниях (вертикальные при О тоже равны).
Из подобия следут отношение
АО:ОС=АD:ВС
(12-х):х=24:16⇒
192=40х
х=4,8
ОС=4,8 см
АО=12-4,8=7,2 см
Примем ОС=х, тогда АО=12-х
Накрестлежащие углы в этих треугольниках равны⇒
∆ АОD ~ ∆ ВОС по двум равным углам при основаниях (вертикальные при О тоже равны).
Из подобия следут отношение
АО:ОС=АD:ВС
(12-х):х=24:16⇒
192=40х
х=4,8
ОС=4,8 см
АО=12-4,8=7,2 см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mtv99
Предмет: Химия,
автор: vlad11303
Предмет: Геометрия,
автор: pirozok278
Предмет: Геометрия,
автор: дома
Предмет: Математика,
автор: kostya01