Question

При каких значениях параметра а уравнение а=-x^3+3x+2 имеет два корня.

Answer 1

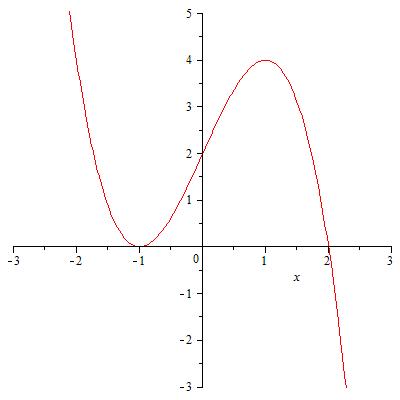
Задача проще, чем кажется:) Сначала надо представить график функции
у = -x^3+3x+2 - это кубическая парабола. у = а - горизонтальная прямая.
прямая пересекает параболу - количество точек пересечения может быть такое: 1, 2 или 3. Две точки пересечения - значит, что у исходного уравнения тоже два решения. Две точки пересечения могут быть только в тех точках, где производная равна нулю.:
у = -x^3+3x+2
y' = -3x^2+3
y' = 0 при х = 1 и х = -1 (это точки экстремума, видно на графике)
а = у(х) = у(-1) = 0
а = у(х) = у(1) = 4

Ответ: а = 0 и а = 4.