Средняя линия равнобедренной трапеции равна 8, угол при одном из оснований равен 135 градусов, а боковая сторона равна 5. Найдите площадь трапеции.
Ответы
1)S трап. = (AD + BC)·BH/2
2) Учитывая, что средняя линия MN = 8 и MN = (AD + BC)/2, то
S трап. = 8·BH
ВН - ?
3) Из ΔАВН - прям . равнобедр.: АН = ВН = 5/√2 = 2,5·√2
!!! В равнобедренном прям. тр-ке катеты отличаются от гипотенузы в √2 раз.
Тогда S трап. = 8·BH = 8·2,5√2 = 20√2(кв.ед.).
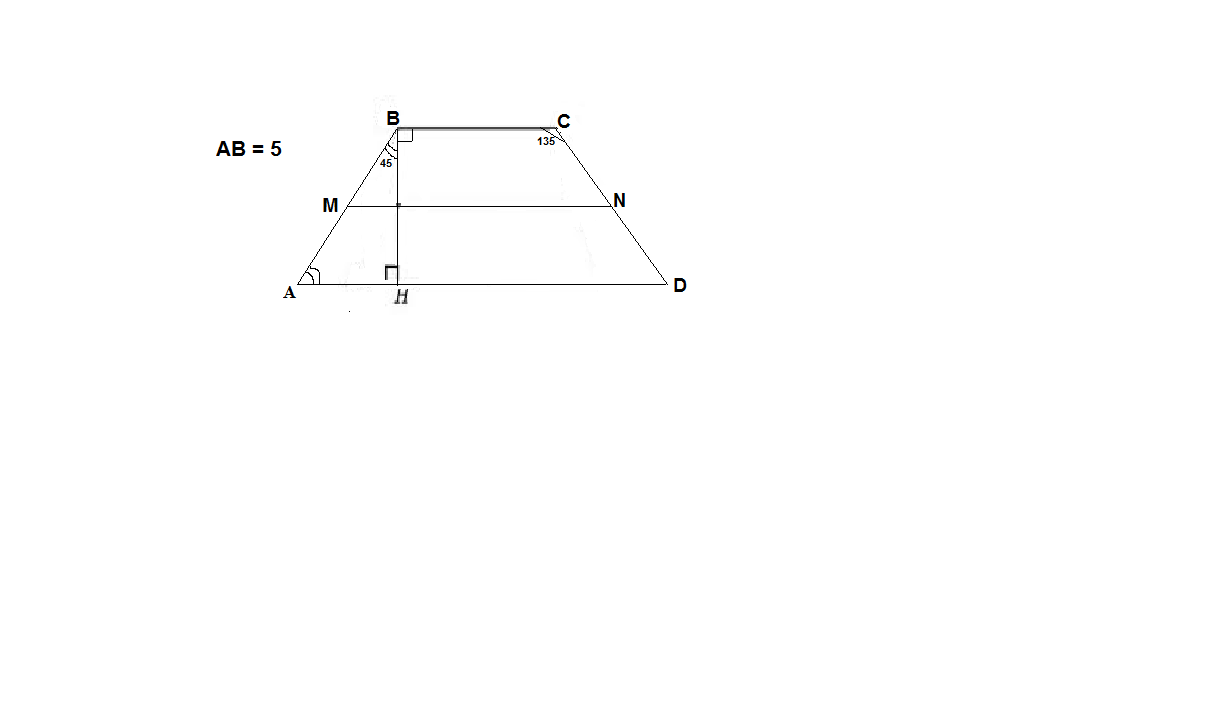
Как мы помним, сумма углов трапеции при ее боковой стороне равна 180 градусов.
Поэтому угол при большем основании равен
180-135=45 градусов.
Опустим высоту на большее основание из угла, равного 135 градусов.
Получим равнобедренный прямоугольный треугольник, в котором гипотенуза равна 5, а высота = второму катету ( части основания)
По формуле диагонали квадрата d=а√2
5=h√2
Отсюда высота, равная второму катету этого треугольника, равна
h=5:√2 или 5√2 :2
S=(8*5√2):2=20 √2
