Question

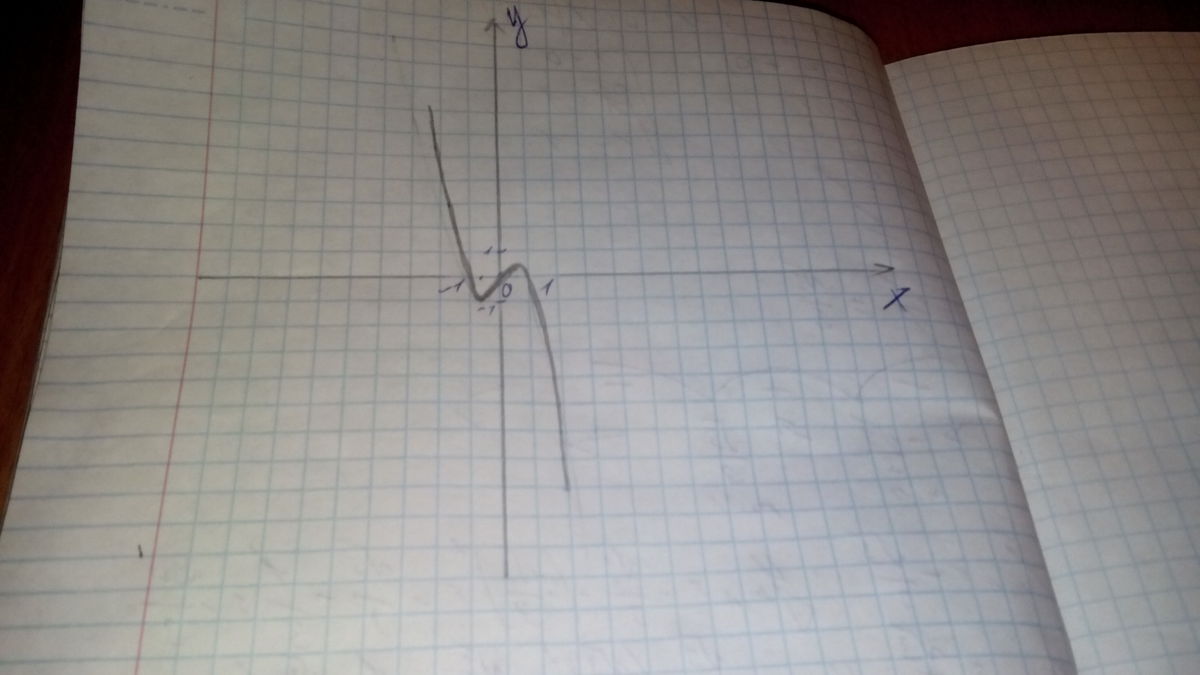
исследуйте функцию y=x-x^3 на монотонность и экстремумы и постройте ее график

Answer 1

y=x-x³
Dy=(-oo;+oo)
нули функции:
x-x³=0
х(1-х²)=0
х=0
х=1
х=-1
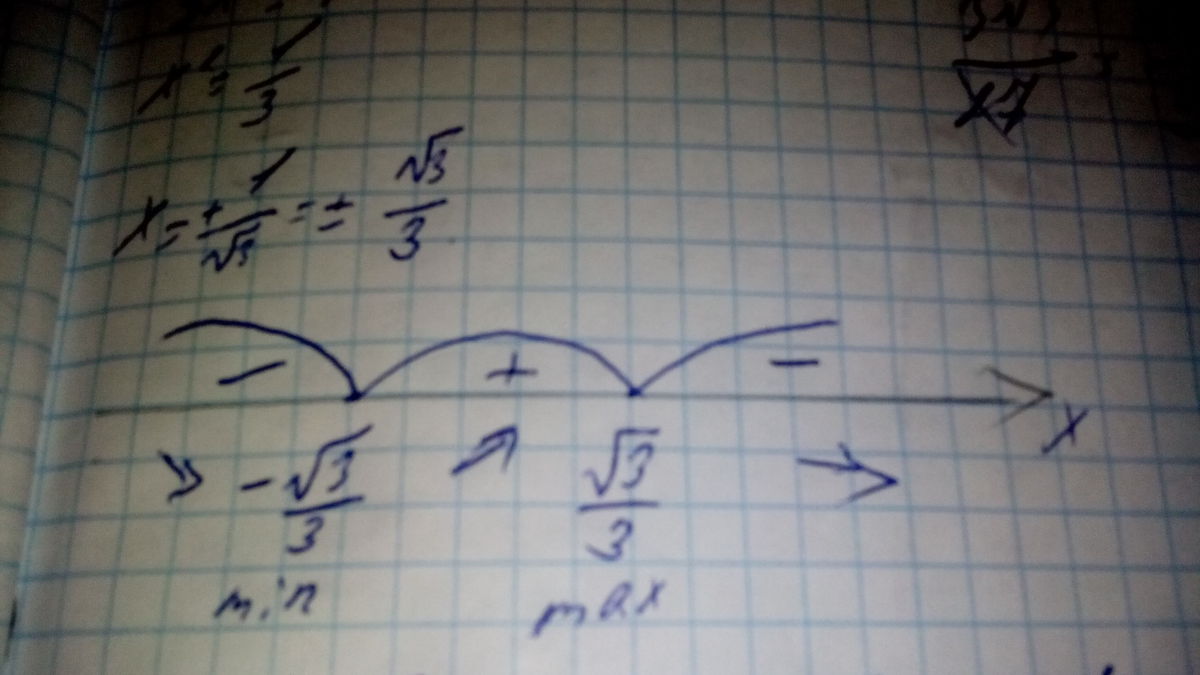
y'=1-3x²
1-3x²=0
3x²=1
x=+-√(1/3)=+-√3/3
Xmax=√3/3;Ymax=√3/3-(√3/3)³=√3/3 - √3/9=2*√3/9
Хmin=-√3/3; Ymin=-√3/3-(√3/3)³=-√3/3 - √3/9=-4*√3/9
Ф-ция убывает на промежутке (-оо;-√3/3) и на (√3/3;+оо),
ф-ция возрастает на [-√3/3;√3/3]