Предмет: Геометрия,
автор: viazhiga
Апофема правильной четырёх уголной
Апофема правильной четырёх уголной призмы NPRST равна 12, радиус окружности , описанной около основания, равен 6. Найдите косинус двугранного угла при основании пирамиды.
Ответы
Автор ответа:
0
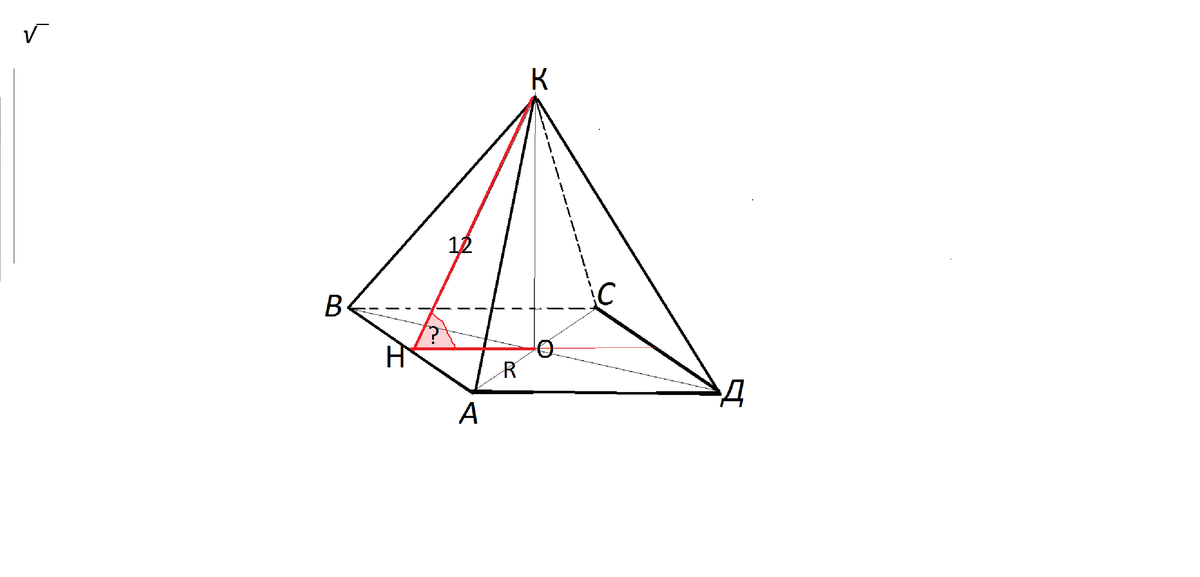
Апофема правильной четырехугольной пирамиды равна 12, радиус окружности, описанной около основания, равен 6. Найдите косинус двугранного угла при основании пирамиды.
-------------------------
Основание правильной четырехугольной пирамиды - квадрат.
Радиус описанной вокруг квадрата окружности равен половине диагонали квадрата.
Пусть основание - АВСД.
Центр описанной окружности квадрата находится в точке пересечения его диагоналей и является основанием КО - высоты пирамиды.
Радиус описанной окружности АО=ОВ, апофема - КН.
Из прямоугольного треугольника АОВ сторона АВ по т. Пифагора равна 6√2.
Косинус двугранного угла при основании пирамиды найдем из прямоугольного треугольника КНО
cоs∠КНО=ОН:КН.
ОН - высота и медиана равнобедренного прямоугольного ⊿ АОВ и равна АН
ОН=АВ:2=6√2:2=3√2
cоs∠КНО=(3√2):12= (√2):4 или иначе 1:(2√2)
Приложения:
Похожие вопросы