Предмет: Математика,
автор: nurikvaliev
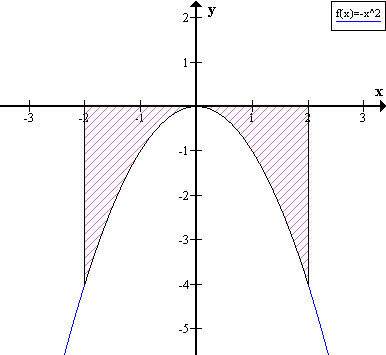
Вычислить площади фигур ограниченных линиями сделав рисунок y=0 y=-x^2 x=-2 x=2
f(x)=-x^2-2x и y=0
Ответы
Автор ответа:
0
1) 
Знак "-" показывает, что площадь считается ниже оси Х
Ответ:
==============================
2)
Ответ:
Знак "-" показывает, что площадь считается ниже оси Х
Ответ:
==============================
2)
Ответ:
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: ivannabondar0
Предмет: Математика,
автор: zlatana12
Предмет: Геометрия,
автор: alpha3nashedi
Предмет: Алгебра,
автор: Fleurety
Предмет: Алгебра,
автор: Mari1795