Question

В прямоугольном треугольнике, биссектриса меньшего угла, образует с меньшим катетом углы, один из которых на 20 градусов больше  другого.Найдите острые углы треугольника.

Answer 1

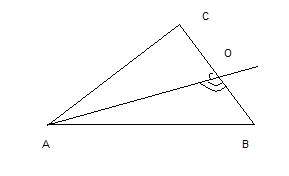
1. Пусть угол СОА, который образует биссектриса с катетом СВ будет х, тогда угол ВОА х+20.
Сумма этих двух углов должна быть равна 180°. Запишем уравнение:
х + (х+20) = 180
2х+20 = 180
2х = 160
х = 80
Итак, <COA = 80°, <BOA = 80+20 = 100°
2. В треугольнике СОА находим угол САО, зная, что сумма углов треугольника равна 180°:
<CAO = 180 - <C - <COA = 180 - 90 - 80 = 10°
3. Поскольку АО - биссектриса, то угол А треугольника АВС равен:
 <A = <CAO * 2 = 10 * 2 = 20°
4. Зная угол А и С в АВС, находим неизвестный угол В:
<B = 180 - <C - <A = 180 - 90 - 20 = 70°