Question

Най­ди­те все зна­че­ния a, при ко­то­рых не­ра­вен­ство x^2+(2a+4)x+8a+1<=0не имеет ре­ше­ний

Answer 1

$x^2+(2a+4)x+8a+1leq0;\ D<0;\ D=b^2-4cdot acdot c=(2a+4)^2-4cdot1cdot(8a+1)=\ =4a^2+16a+16-32a-4=4a^2-16a+12<0;\ a^2-4a+3<0;\ a^2-4a+3=0; D_1=16-12=4=(pm2)^2;\ a_1=frac{4-2}{2}=frac{2}{2}=1;\ a_2=frac{4+2}{2}=frac{6}{2}=3;\ 1<a<3;\<span>ainleft(1;3right).$
при 1<a<3 дискриминант нашего уравнения отрицательный, значит уравнение не имеет решений
Ответ: $left(1;3right).$

Answer 2

Ответ:    а ∈ (1 ; 3)

Объяснение:

x² + (2a + 4)x + 8a + 1 ≤ 0

Левая часть выражения - квадратичная функция, графиком которой является парабола с ветвями, направленными вверх (коэффициент перед х² равен 1, положительный).

Неравенство не будет иметь решений, если парабола не будет пересекать ось Ох, т.е. квадратный трехчлен не будет иметь корней. А он не имеет корней, если дискриминант отрицательный.

Поэтому составим выражение для дискриминанта и решим неравенство D < 0.

D = (2a + 4)² - 4 · (8a + 1) = 4a² + 16a + 16 - 32a - 4 = 4a² - 16a + 12

4a² - 16a + 12 < 0

a² - 4a + 3 < 0

Решаем методом интервалов:

Найдем нули:

a² - 4a + 3 = 0

D/4 = 4 - 3 = 1

a₁ = 2 - 1 = 1

a₂ = 2 + 1 = 3

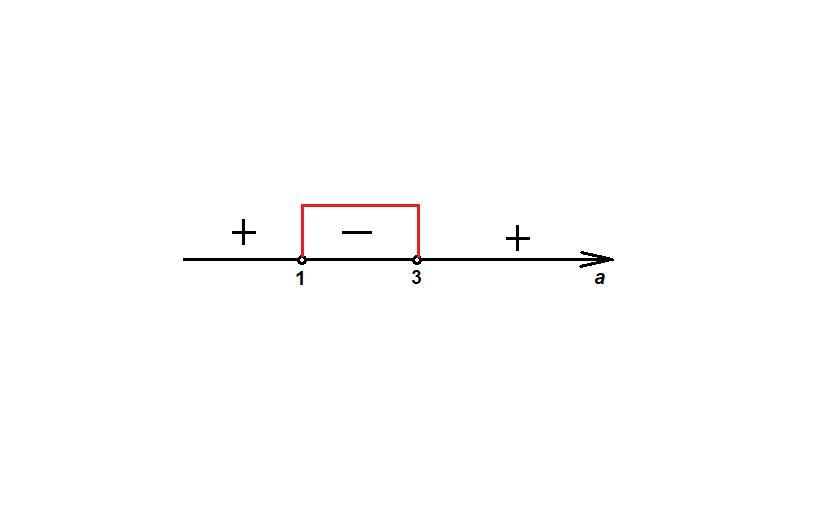
Отметим точки на координатной прямой (см. рисунок).

Решение неравенства а ∈ (1 ; 3).