Question

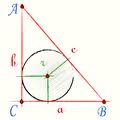
в прямоугольном треугольнике вписана окружность радиуса r. Найдите периметр треугольника, если: а) гипотенуза равна 26 см, r=4 см; б)точка касания делит гипотенузу на отрезки, равные 5 см и 12 см

Answer 1

Обозначения обычные - a и b катеты, c гипотенуза.

 

1. a + b - c = 2*r; P = 2*r + 2*c = 2*(r + c) = 2*30 = 120;

2. c = 17; a = 5 + r; b = 12 + r;

a^2 + b^2 = c^2;

17^2 = (5 + r)^2 + (12 + r)^2;

r^2 + 17*r - 60 = 0; r = 3; (решение  r = -20 отбрасываем) 

а = 8; b = 15;      (8, 15, 17 - Пифагорова тройка)

P = 40;

Answer 2

1) !!!Радиус, вписанной в прямоугольный тр-к ,окружности равен:

  r = (a+b-c)/2 , где а,b - катеты, с - гипотенуза, тогда

  4 = (а+b -26)/2

  а+b -26 = 8

  а+b  = 34

Таким образом Р = а+b +с =34+26 =60 (см).

2) Правило:
   отрезки  касательных к окружности, проведённые из одной точки, равны, т.е.

    ВМ =ВР=5,    АМ=АТ=12, СТ=СР = х, тогда по теореме Пифагора:

    (5 + х)²+(12 + х)²=17²

     25 + 10х + х² +144 +24х +х² = 289

     2·х² +34х+169 - 289 =0

     2·х² +34х -120 =0

      х² + 17х -60 =0

      х₁ = 3;    х₂= -20 ( не подходит по смыслу задачи)

 Таким образом АС = 15, ВС = 8  и Р= 15+8+17 = 40 (см).