диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол 60 градусов. Найдите отношение объемов конуса и шара.
Ответы
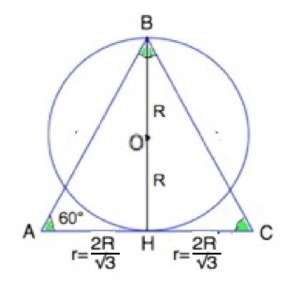
Сделаем схематический рисунок осевого сечения конуса и шара так, чтобы высота конуса наложилась на диаметр шара, при этом они совпадут ( равны по условию),
Осевое сечение шара - круг, конуса - треугольник, в данном случае - равносторонний треугольник, т.к. образующая составляет с плоскостью основания угол 60°.
Примем радиус шара равным R. Тогда высота конуса BH=2 R.
Высота ( она же медиана и биссектриса) делит равносторонний треугольник АВС на два равных прямоугольных с острыми углами ВАН=ВСН=60°.
Радиус основания конуса=АН=СН= ВН:tg60°=2R:√3
V (к)=πr•h:3=π(2R/√3)²•2R/3
V(к)=8πR³/9
V(ш)=4πR³:3
Искомое отношение V (кон):V(шара)
(8πR³/9):(4πR³:3)=(8πR³•3):(9•4πR³)=2:3