Question

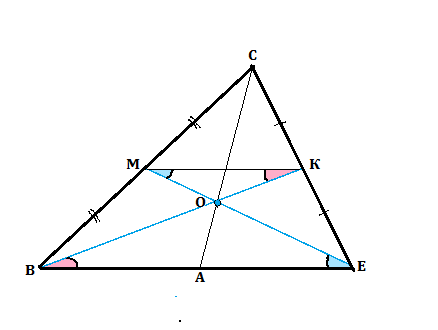
Медианы BK и EM треугольника ВСЕ пересекаются в точке О. Докажите что: 1). треугольники КОМ и ВОЕ подобны. 2). площадь МОК : площ.СМК = 1:3

Answer 1

1) ВК и ЕМ - медианы. ⇒ ВМ=МС и ВЕ=КС ⇒
 МК - средняя линия треугольника ВСЕ. ⇒ 
МК||ВЕ 
∠ЕМЕ=∠МЕВ и  ∠МКВ=∠КВЕ как накрестлежащие при пересечении параллельных прямых МК и ВЕ секущими ВК  и МЕ.
 МК=ВЕ:2, k=1/2 ⇒
∆ МОК~∆ ВОЕ , ч.т.д.
-------------
2) Медианы треугольника делят его на равновеликие треугольники. 
Ѕ ∆ ВОЕ=Ѕ ∆ СОВ=Ѕ ∆ СОЕ= Ѕ ∆ ВСЕ:3 
Так как МК - средняя линия, ∆ СМК~∆ ВСЕ, и k=1/2 
Площади подобных фигур относятся, как квадрат коэффициента их подобия. 
Ѕ ∆ МСК:Ѕ ВСЕ=k²=1/4 
Коэффициент подобия ∆ МОК и ∆ ВОЕ=1/2 
Ѕ ∆ МОК: Ѕ ∆ ВОЕ=1/4 
Так как Ѕ ∆ ВОЕ= Ѕ ∆ ВСЕ:3, то 
Ѕ ∆ МОК: Ѕ ∆ ВСЕ:3=Ѕ ∆ ВСЕ/12 
Так как Ѕ ∆ МСК=Ѕ ВСЕ/4, то 
Ѕ ∆ МОК: Ѕ ∆ СМК=(Ѕ ∆ ВСЕ/12):(Ѕ ∆ ВСЕ/4)=1/3, ч.т.д.