Предмет: Алгебра,
автор: vinitnei
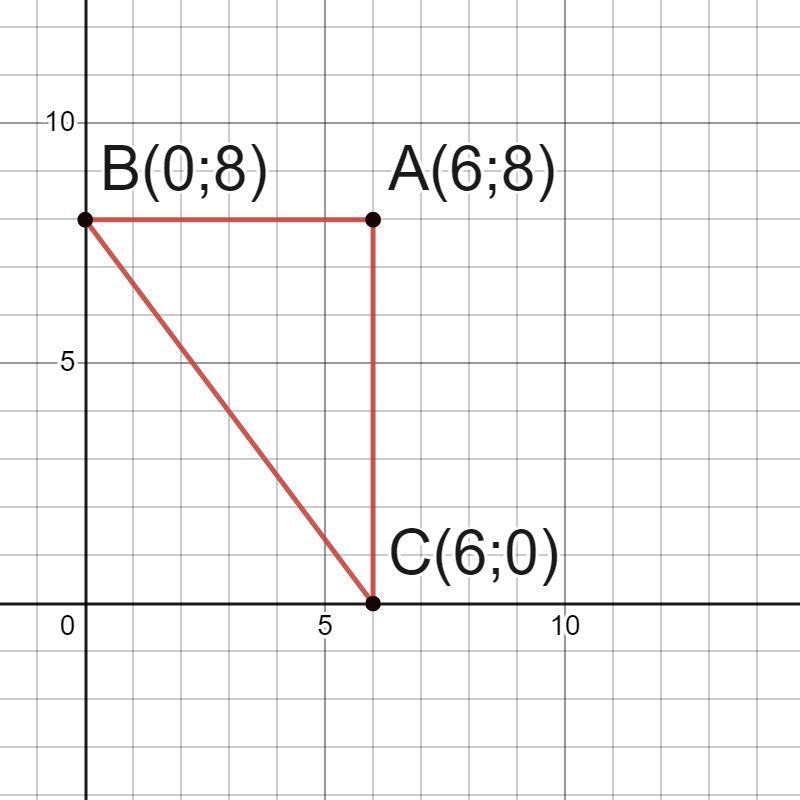
Трикутник ABC заданий координатами верши A(6; 8), B(0; 8), C(6; 0). Знайдіть площу трикутника.
Помогиииите
Ответы
Автор ответа:
0
Ответ: S=24 кв. ед.
Объяснение:
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: dariyka2008
Предмет: Химия,
автор: hanminheill
Предмет: Алгебра,
автор: vasilcenkoangelina1
Предмет: Обществознание,
автор: nosttyya
Предмет: Қазақ тiлi,
автор: zolbulatasela