Предмет: Геометрия,
автор: lera3211
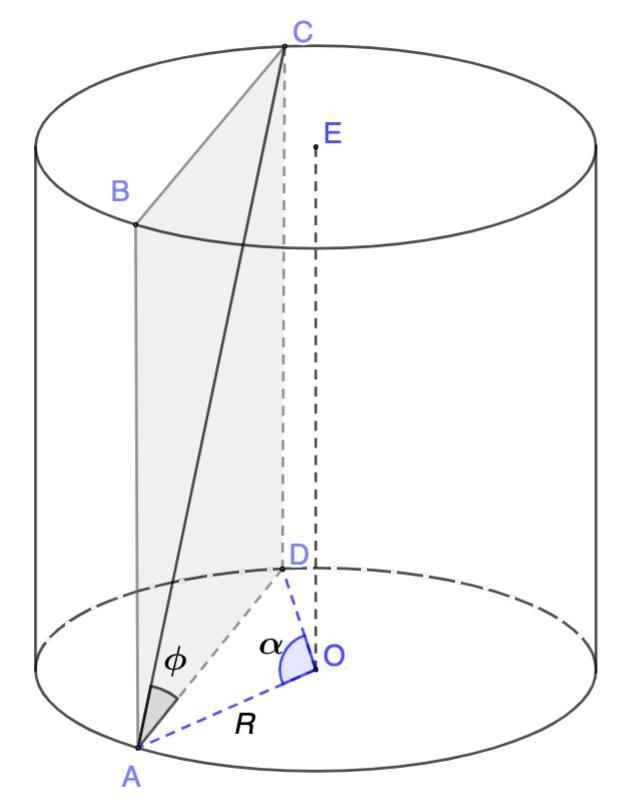
В цилиндре параллельно его оси проведено сечение, диагональ которого образует с плоскостью основания угол ф. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна а, 0° < а < 180°. Найдите площадь сечения, если радиус основания цилиндра равен R.
пожалуйста, помогите
Ответы
Автор ответа:
2
Ответ:
Площадь сечения равна R²tg φ (2 - 2cos α) ед².
Объяснение:
В цилиндре параллельно его оси проведено сечение, диагональ которого образует с плоскостью основания угол φ. Это сечение пересекает основание по хорде, стягивающей дугу, градусная мера которой равна α, 0° < α < 180°. Найдите площадь сечения, если радиус основания цилиндра равен R.
Дано: цилиндр;
ABCD - сечение; ABCD || OE;
АС - диагональ; ∠CAD = φ;
R - радиус основания;
◡AD = α; 0 < α < 180°
Найти: S(ABCD)
Решение:
- Центральный угол равен градусной мере дуги, на которую он опирается.
⇒ ∠AOD = α
Рассмотрим ΔAOD - равнобедренный (OA = OD = R)
Найдем AD по теореме косинусов:
- Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
⇒ AD² = OA² + OD² - 2OA · OD · cos α
AD² = R² + R² - 2R² cos α = R²(2 - 2cos α)
⇒
Рассмотрим ΔACD - прямоугольный.
- Тангенс угла - отношение противолежащего катета к прилежащему.
- Площадь прямоугольника равна произведению смежных сторон.
S(ABCD) = AD · CD =
#SPJ1
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: sofideniz486
Предмет: История,
автор: arinasen9
Предмет: История,
автор: td6279841
Предмет: Другие предметы,
автор: HamenLine
Предмет: Английский язык,
автор: artemgercynov004