Предмет: Геометрия,
автор: bahmackijdanila
Помогите найти угол между прямой и плоскостью
Приложения:
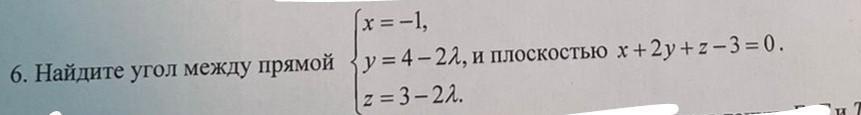
Ответы
Автор ответа:
1
Ответ: 60 градусов.
Объяснение:
Найдем угол между прямой
x = - 1
y = - 2t + 4
z = - 2t + 3
и плоскостью x + 2y + zz - 3 = 0.
Направляющий вектор прямой имеет вид:
s = (0; -2; -2).
Вектор нормали плоскости имеет вид:
q = 1; 2; 1
Вычислив угол между векторами, найдем угол между прямой и плоскостью:
sin φ = |cos ψ| = | s · q |/| s |·| q | =
= | sx · qx + sy · qy + sz · qz |/√(sx² + sy² + sz²) · √(qx² + qy² + qz²) =
= | 1 · 0 + 2 · (-2) + 1 · (-2) |/√(1² + 2² + 1²) · √(0² + (-2)² + (-2)²) =
= | 0 - 4 - 2 |/√(1 + 4 + 1) · √(0 + 4 + 4) =
= 6/(√6 ·√8) = 6/√48 = √3/2 ≈ 0.866.
φ = 60°.
Похожие вопросы
Предмет: МХК,
автор: denisgavrilcenko0
Предмет: Математика,
автор: valiaaleshina87
Предмет: Математика,
автор: satibaldieva2023
Предмет: Алгебра,
автор: Kopcheniy
Предмет: Английский язык,
автор: polina50208