Предмет: Алгебра,
автор: Dianatishenko394
Помогите пожалуйста решить 3 и 5 задания
Приложения:
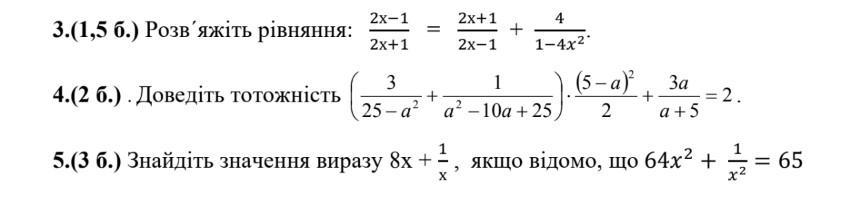
Ответы
Автор ответа:
1
Объяснение
3.
ОДЗ:
(2х+1)*(2х-1)≠0
х₁≠-0,5 х₂≠0,5
x=0,5∉ОДЗ ⇒
Ответ: уравнение не имеет решения.
5.
Похожие вопросы
Предмет: Литература,
автор: varausenko826
Предмет: Українська мова,
автор: natalya32sss
Предмет: Математика,
автор: stepchenko81
Предмет: Физика,
автор: katerinzzzz
Предмет: Математика,
автор: Аноним