Предмет: Геометрия,
автор: Michael2010
Очень срочно!!!! 50 баллов!
Треугольник ABC вписан в окружность.
Угол ABC = 36 градусов. Найдите углы треугольника AОС, если О - центр окружности.
Приложения:
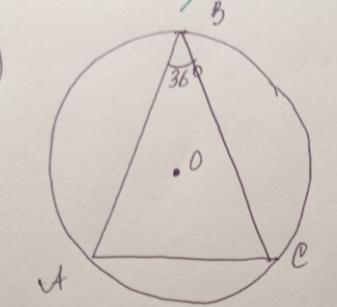
natiart06:
а больше ничего нет в условии?
Нет , больше ничего не дали
там можно только угол АОС найти
Если дочертить треугольник то получится что надо найти углы треугольника aoc - a, o и c
для нахождения всех углов мало данных
Я за эту роботу получила 11 балов
Ответы
Автор ответа:
1
Ответ:
∠АОС=72°; ∠ОАС=54°; ∠ОСA=54°
Объяснение:
∠АОС=2*∠АВС=2*36°=72° (центральний кут в два рази більше відповідного вписаного кута)
АО=ОС=R- радіуси.
∆АОС- рівнобедрений трикутник.
Сума кутів трикутника дорівнює 180°; В рівнобедреному трикутнику кути при основі рівні.
∠OАC=∠OCA;
∠OАC=(180°-∠АОС)/2=(180°-72°)/2=54°
∠OCA=54°
Приложения:
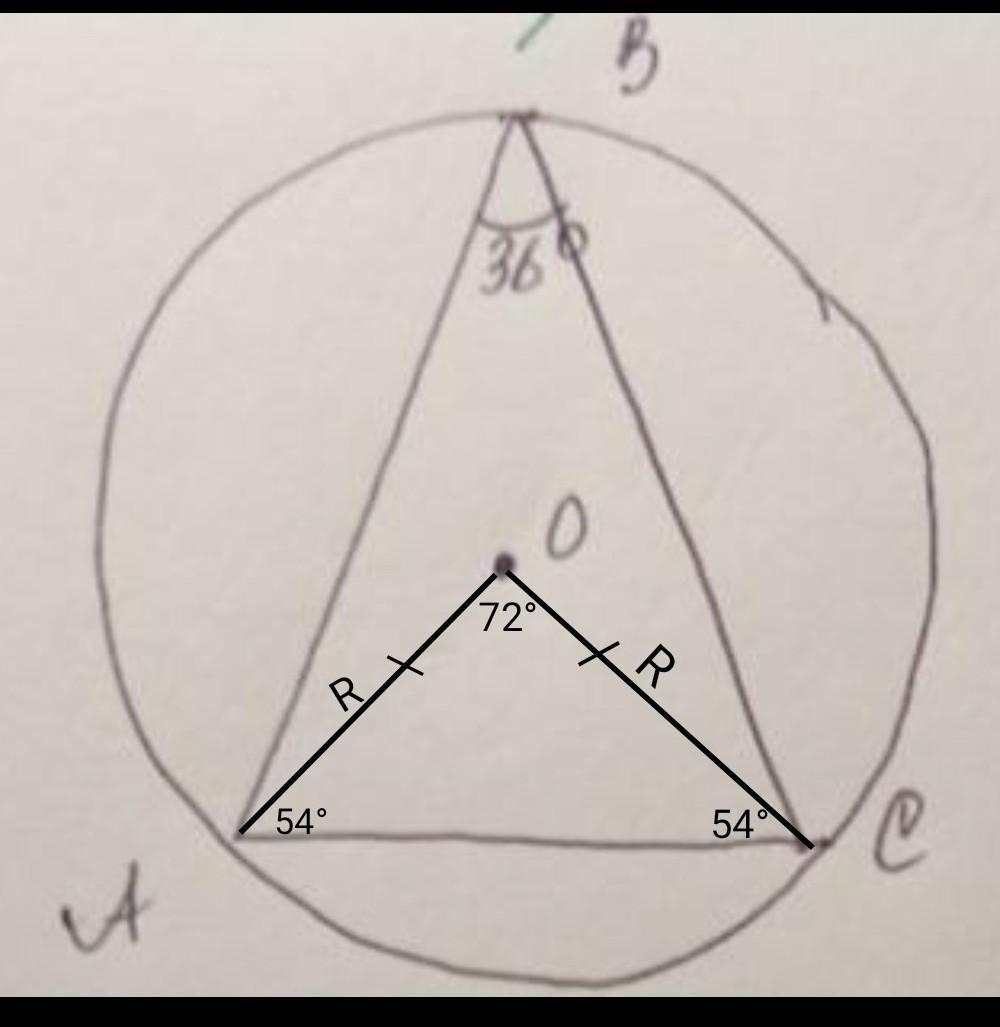
Я все решила, что еще нужно?
Спасибо большое!!! Больше ничего не нужно.
Автор ответа:
1
Если треугольник ABC вписан в окружность, то угол AOC, где O - центр окружности, равен удвоенной мере угла внешней дуги, которую образует сторона AC.
Таким образом, угол AOC = 2 * угол ABC = 2 * 36 градусов = 72 градуса.
Так как треугольник ABC вписан в окружность, сумма всех углов треугольника равна 180 градусов. Так что, если угол ABC = 36 градусов, то угол AOC + угол BOC = 180 градусов.
Отсюда угол BOC = 180 градусов - 72 градуса = 108 градусов.
Таким образом, углы треугольника AOC равны 72 градуса и 108 градусов.
Таким образом, угол AOC = 2 * угол ABC = 2 * 36 градусов = 72 градуса.
Так как треугольник ABC вписан в окружность, сумма всех углов треугольника равна 180 градусов. Так что, если угол ABC = 36 градусов, то угол AOC + угол BOC = 180 градусов.
Отсюда угол BOC = 180 градусов - 72 градуса = 108 градусов.
Таким образом, углы треугольника AOC равны 72 градуса и 108 градусов.
Похожие вопросы
Предмет: Химия,
автор: duisenabdurohman
Предмет: Математика,
автор: bahazievarailyam01
Предмет: Қазақ тiлi,
автор: fpolatkyzy
Предмет: Математика,
автор: roxygame2008