Предмет: Алгебра,
автор: zhunisbekmansur
5. Вычислите: x_{1} ^ 2 + x_{2} ^ 2 , если известно, что x_{1} , x_{2} - корни квадратного уравнения x ^ 2 + 11x + 10 = 0 (5 баллов)
даю 100 баллоов срочно нужно
Приложения:
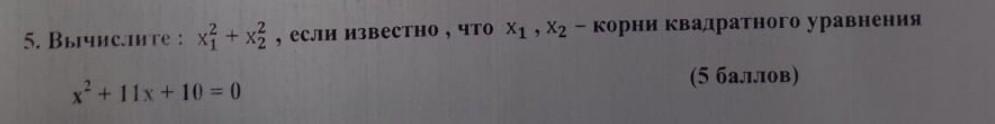
Ответы
Автор ответа:
0
Если , то первый корень равен
, а второй
, следовательно, уравнение
имеет два корня:
zhunisbekmansur:
можно полный ответ
А это какой?
мы 8 класс и это не проходили
только квадратное уравнение прошли
Что не проходили? Так я написал, как решать, что тут проходить? Числа подставлять и всё? Ну а я какое уравнение решил, кубическое?
ок ,главное чтобь правильно было
однако, 1+11+10 != 0
а, всё правильно
Автор ответа:
0
Ответ:
101
Объяснение:
Сначала решим уравнение:
Чтобы найти значение выражения , просто подставим
:
Следовательно, ответ будет равным 101.
другой способ
x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(-b/a) ^2-2*c/a=b^2/a^2-2c/a=(b^2-2ac)/a^2
x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=(-b/a) ^2-2*c/a=b^2/a^2-2c/a=(b^2-2ac)/a^2
Похожие вопросы
Предмет: Английский язык,
автор: zlatazvyaginceva
Предмет: Алгебра,
автор: a65247237
Предмет: Українська мова,
автор: ulia297
Предмет: Английский язык,
автор: kmm10
Предмет: Химия,
автор: marencochannel838