Question

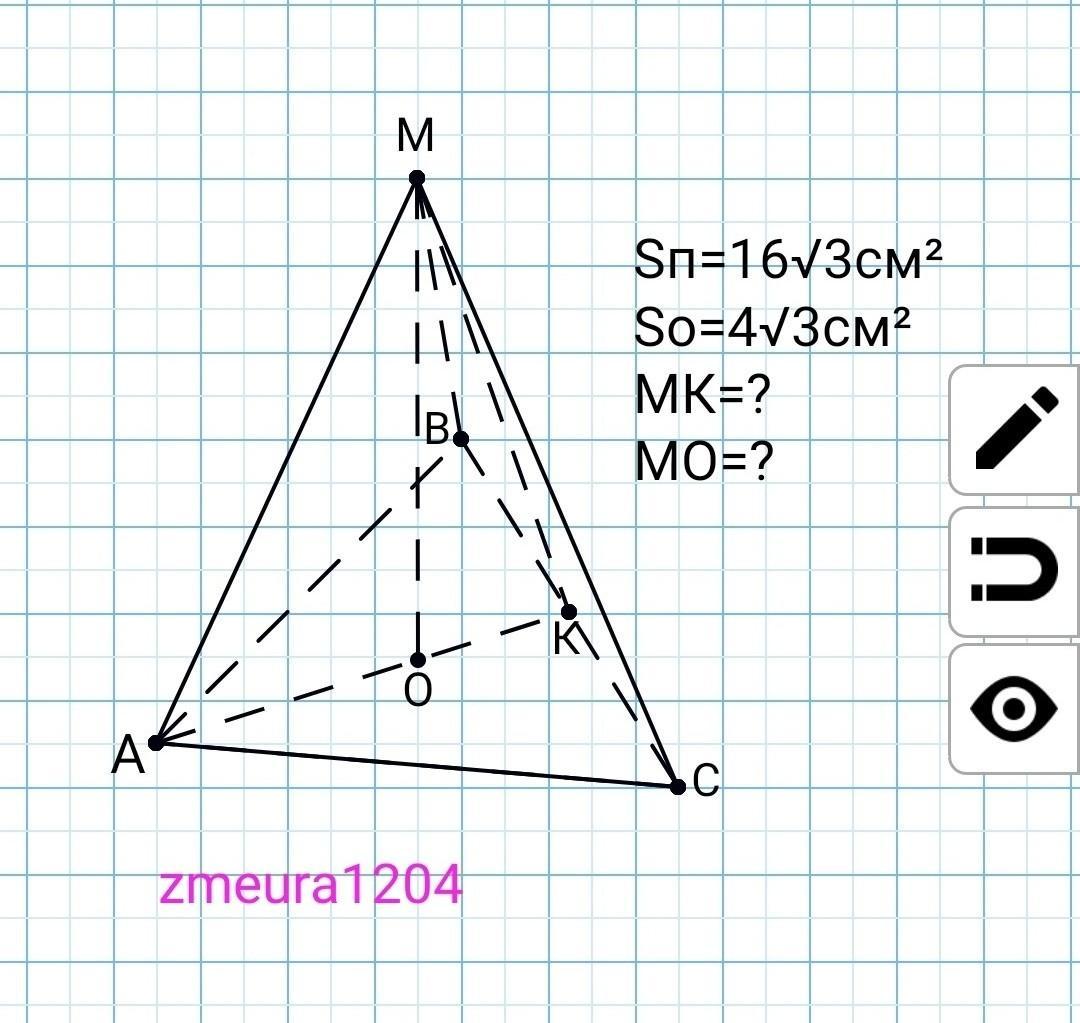
В правильной треугольной пирамиде полная поверхность равна 16√3 см², а площадь основания 4√3 см². Найдите апофему, высоту пирамиды. ПОМОГИТЕ ПОЖАЛУЙСТА, СРОЧНО!!!​

Answer 1

Ответ:

Апофема равна 2√3см

Высота пирамиды равна √(70/3)см

Объяснение:

So=AB²√3/4; →

AB=√(4*So/√3)=√(4*2√3/√3)=2√2см.

Sп=So+Sб; →

Sб=Sп-So=16√3-2√3=14√3см²

Ро=3*АВ=3*2√2=6√2см

Sб=½*Ро*МК; →

МК=2*Sб/Po=2*14√3/6√2=

=7√6/3см

_____________

r=OK;

r=AB/2√3=2√2/2√3=√6/3см

∆МКО- прямоугольный треугольник.

Теорема Пифагора:

МО=√(МК²-ОК²)=√((7√6/3)²-(√6/3)²)=

=√(294/9-6/9)=√(288/9)=

=12√2/3=4√2см