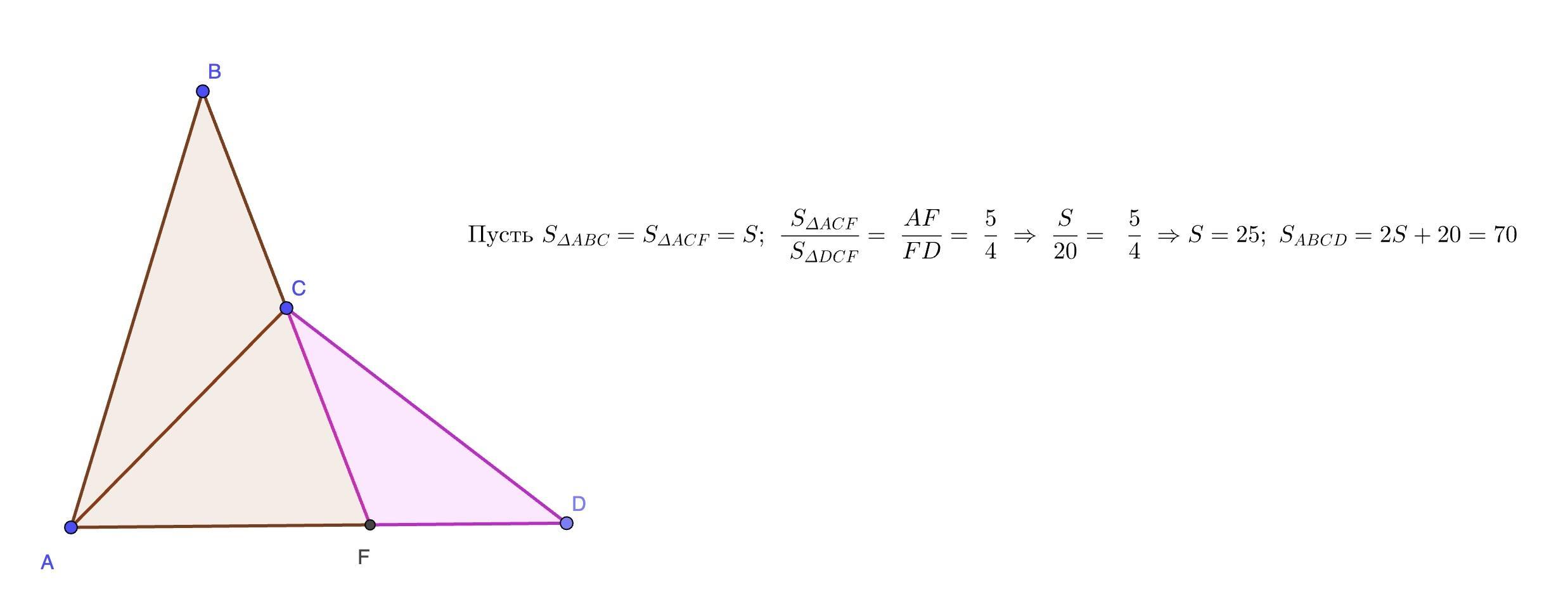
(Даю 50 баллов )В невыпуклом четырехугольнике АВСД продолжение стороны ВС за точку С пересекает сторону АД в точке F так, что АF:FД-5:4, точка С-середина отрезка BF. Найдите площадь четырехугольника АВСД если площадь треугольника РСД равна 20 см2
Ответы
Ответ:
Площадь ABCD равна 70 см².
Объяснение:
В невыпуклом четырехугольнике АВСD продолжение стороны ВС за точку С пересекает сторону АD в точке F так, что АF:FD=5:4, точка С-середина отрезка BF. Найдите площадь четырехугольника АВСD, если площадь треугольника FСD равна 20 см².
Дано: ABCD - невыпуклый четырехугольник;
ВС ∩ AD = F; AF : FD = 5 : 4;
BC = CF; S(FCD) = 20 см².
Найти: S(ABCD)
Решение:
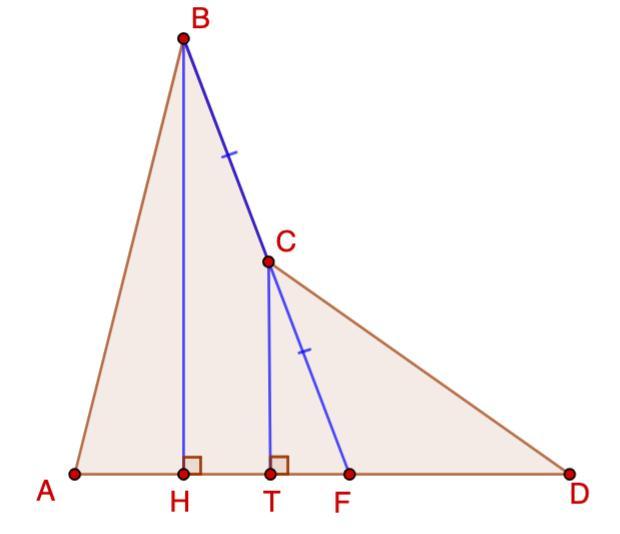
Проведем ВН ⊥ AD; CT ⊥ AD.
Рассмотрим ΔНВF - прямоугольный.
- Если две прямые перпендикулярны третьей, то они параллельны между собой.
⇒ ВН || CT.
BC = CF (условие)
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.
⇒ СТ - средняя линия ΔНВF.
- Средняя линия равна половине стороны, которую она не пересекает.
Пусть СТ = h ⇒ BH = 2h
AF : FD = 5 : 4
Пусть AF = 5x, тогда FD = 4x
Рассмотрим ΔFCD.
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
⇒
Рассмотрим ΔABF.
S( ABCD) = S(FCD) + S(ABF) = 20 + 50 = 70 (см²)
#SPJ1
Ответ: 70
Объяснение:
Отношение площадей треугольников с равными высотами равно отношению сторон , к которым эти высоты проведены