Предмет: Алгебра,
автор: assasen36
дана геометрическая прогрессия {bn}
b6-b4=1700; b5-b3=340. найдите b1 и q
Ответы
Автор ответа:
1
Ответ:
Для решения этой задачи нам нужно использовать формулы для нахождения членов геометрической прогрессии.
Пусть b1 - первый член прогрессии, а q - знаменатель прогрессии.
Так как b6 = b4 * q^2 и b5 = b3 * q, мы можем записать уравнения:
b4 * q^2 - b4 = 1700
b3 * q - b3 = 340
Теперь мы можем выразить b4 и b3 через b1 и q:
b4 = b1 * q^3
b3 = b1 * q^2
Подставим эти значения в уравнения:
b1 * q^3 * q^2 - b1 * q^3 = 1700
b1 * q^2 * q - b1 * q^2 = 340
Разделим оба уравнения на b1:
q^5 - q^3 = 1700 / b1
q^3 - q = 340 / b1
Теперь мы можем решить эти уравнения относительно q. После этого можно найти b1, используя найденное значение q.
Объяснение:
Автор ответа:
0
Ответ:
надеюсь помогла
b¹= 17/30
q= 5
Приложения:
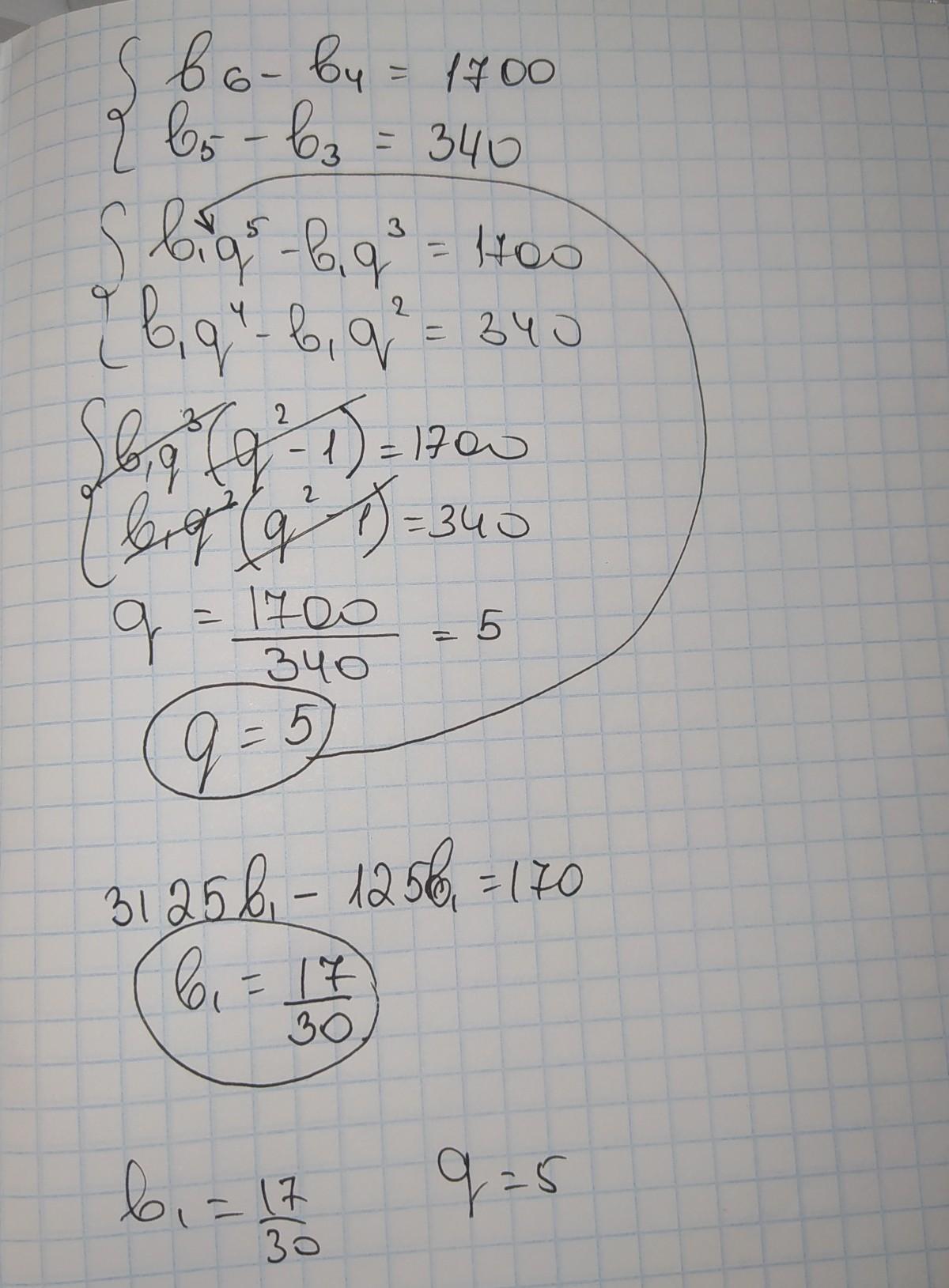
hellokookooko123:
там вместо 170. 1700 я неправильно написала просто 0 забыла написать
Похожие вопросы
Предмет: Українська мова,
автор: artemplekhov
Предмет: Қазақ тiлi,
автор: ilyas2011zhenisbek
Предмет: История,
автор: amiribraev140
Предмет: Обществознание,
автор: gods1dy
Предмет: Алгебра,
автор: khabibullaevshohjaho