Предмет: Алгебра,
автор: jaahaa200000
Решите уравнение по Алгебре
Приложения:
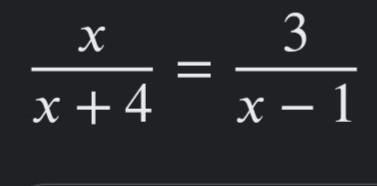
Ответы
Автор ответа:
0
polarkat:
А чего ты только детские задания смотришь?)) На большее не способен?) Ну вот прокомментируйте решение моё https://znanija.com/task/54590016. Очень интересно)) А то способен тут проверять задачки 6 класса и всё)))
Я жду, когда будешь комментировать нормальные задания с решениями, а не просто решить уравнения)) твой максимум что ли?))
Ясно, слито)) иди повыписывай ещё)) забавный мальчик ))
обиженка на эту жизнь,ахахах
Автор ответа:
0
Ответ:
Объяснение:
Перемножим всё крестиком и решим как обычное квадратное уравнение:
Следовательно, у этого уравнения два корня: либо
.
Похожие вопросы
Предмет: Английский язык,
автор: akutagawaatsu
Предмет: Алгебра,
автор: yarikko1991
Предмет: Алгебра,
автор: egorrabhsenko
Предмет: Математика,
автор: genrih777nikita
Предмет: Русский язык,
автор: nastakozyr28