Предмет: Алгебра,
автор: 12lemongames
a + b + 1/a + 1/b ≥ 4, якщо a>0, b>0. Срочно!!!
Приложения:

antonovm:
эта сумма не меньше чем 4 корня 4 степени из произведения ( неравенство Коши ) , а произведение равно 1
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Cогласно неравенства АМ-GM (неравенство Коши)
m+l+x+y≥4
a=m b=l 1/a=x 1/b=y
=> a+b+1/a+1/b≥
=> a+b+1/a=1/b≥4
Автор ответа:
1
Ответ:
Объяснение:
решение на фото
применим неравенство Коши о средних
Приложения:
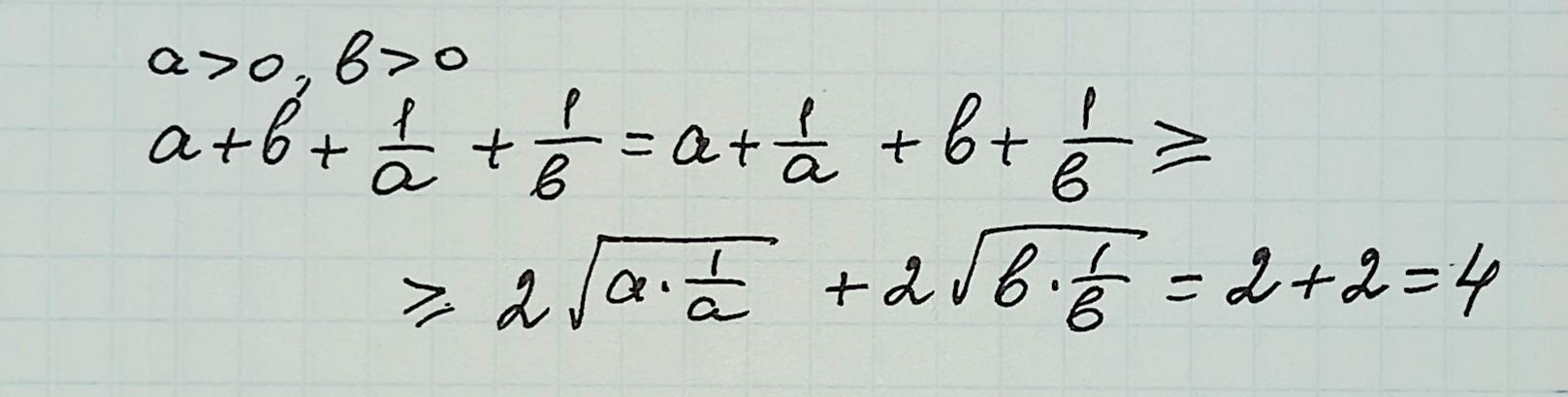
Спасибо
Похожие вопросы
Предмет: Қазақ тiлi,
автор: isagalievagulmira7
Предмет: История,
автор: glebmig
Предмет: Математика,
автор: gu1382343344we
Предмет: Математика,
автор: k877768003038
Предмет: Биология,
автор: bakow91kz