Дано уравнение x^2-7x-12=0. x1 и x2 - корни уравнения. Не вычисляя корней, найдите значение выражения x1/x2+x2/x1. 60 баллов
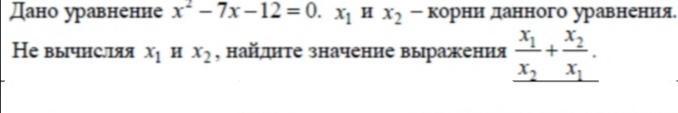
Ответы
Ответ:
значение выражения x1/x2 + x2/x1 равно -73/12.
Объяснение:
Для нахождения значения выражения x1/x2 + x2/x1, мы можем использовать свойство суммы и произведения корней квадратного уравнения.
Из уравнения x^2 - 7x - 12 = 0, мы знаем, чтоумма корней равна -(-7) = 7, а их произведение равно -12.
Теперь рассмотрим выражение x1/x2 + x2/x1. Мы можем заметить, что это выражение равно (x1^2 + x2^2) / (x1 * x2).
Используя свойство суммы и произведения корней, мы можем переписать это выражение как (сумма корней^2 - 2 * произведение корней) / (произведение корней).
Подставляя значения суммы и произведения корней, получаем:
(7^2 - 2 * (-12)) / (-12) = (49 + 24) / (-12) = 73 / (-12) = -73/12.
Ответ:
-6 1/12
Объяснение:
х²-7х-12=0
а=1 ; b= -7 ; c= -12
x1•x2=c/a= -12/1= -12
x1+x2= -b/a= -(-7)/1= 7/1=7
x1/x2+x2/x1=(x1•x1+x2•x2)/(x1•x2)=
=(x1²+x2²)/(x1•x2)=((x1+x2)²-2•x1•x2)/(x1•x2)=
=(7²-2•(-12))/(-12)=(49+24)/(-12)= 73/(-12)=
= -6 1/12