РЕШИТЕ ЧЕРЕЗ лопиталя
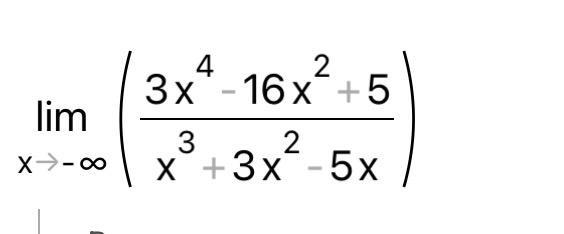
Ответы
Ответ:
Применяем правило Лопиталя . Применяем его 3 раза .
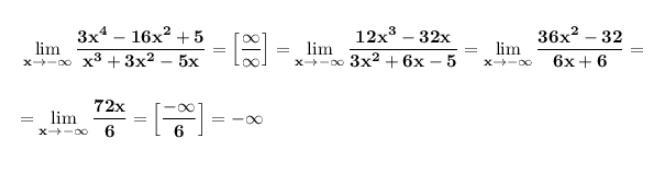
Ответ: предел исходной функции при x, стремящемся к отрицательной бесконечности, равен -∞.
Объяснение:
Чтобы решить эту задачу с помощью правила Лопиталя, мы возьмем производные числителя и знаменателя по переменной x и найдем их пределы, когда x стремится к отрицательной бесконечности.
Начнем с нахождения производных:
f'(x) = (12x^3 - 32x) / (3x^2 + 6x - 5)
g'(x) = (3x^2 + 6x - 5) / (x^3 + 3x^2 - 5x)
Теперь найдем пределы этих производных при x, стремящемся к отрицательной бесконечности:
lim x-> -∞ f'(x) = lim x-> -∞ (12x^3 - 32x) / (3x^2 + 6x - 5) = -∞ / -∞
По правилу Лопиталя, мы можем взять производные числителя и знаменателя снова:
lim x-> -∞ f'(x) = lim x-> -∞ (36x^2 - 32) / (6x + 6) = lim x-> -∞ (36x^2 - 32) / 6x = -∞
lim x-> -∞ g'(x) = lim x-> -∞ (3x^2 + 6x - 5) / (x^3 + 3x^2 - 5x) = -∞ / -∞
Снова применяем правило Лопиталя:
lim x-> -∞ g'(x) = lim x-> -∞ (6x + 6) / (3x^2 + 6x - 5) = lim x-> -∞ (6x + 6) / (6x + 6) = 1
Теперь мы можем рассмотреть предел исходной функции:
lim x-> -∞ (3x^4 - 16x^2 + 5) / (x^3 + 3x^2 - 5x) = lim x-> -∞ f(x) / g(x)
По правилу Лопиталя, это равно:
lim x-> -∞ (f'(x) / g'(x)) = lim x-> -∞ (-∞ / 1) = -∞