Предмет: Математика,
автор: polinalisicina526
ПОМОГИТЕ ПРОШУ!!!!!!!!!!!!!!!!!!!!!!!!!! ОЧ СРОЧНО
Приложения:
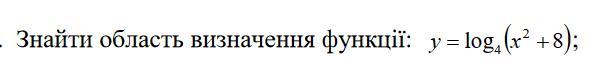
Ответы
Автор ответа:
3
Область определения - вся вещественная прямая, так как аргумент логарифма при всех x будет положительной
Автор ответа:
3
Ответ:
Пошаговое объяснение:
Область значений функции это интервал
, так как
принимает значения от нуля до бесконечности.
Область определения логарифма с положительным основанием - это интервал , так как степень с положительным основанием принимает любые значения, большие нуля.
Мы видим, что , следовательно, какой бы
мы не взяли, логарифм от
будет определяемым, а следовательно, и вся функция тоже.
То есть, ответ: .
Похожие вопросы
Предмет: Математика,
автор: nachnost16011
Предмет: Математика,
автор: slavickoriavko
Предмет: Математика,
автор: zajlaubajnuraj
Предмет: Математика,
автор: sistersanimatedly
Предмет: География,
автор: unkuebaev