Предмет: Математика,
автор: AAAAerfg
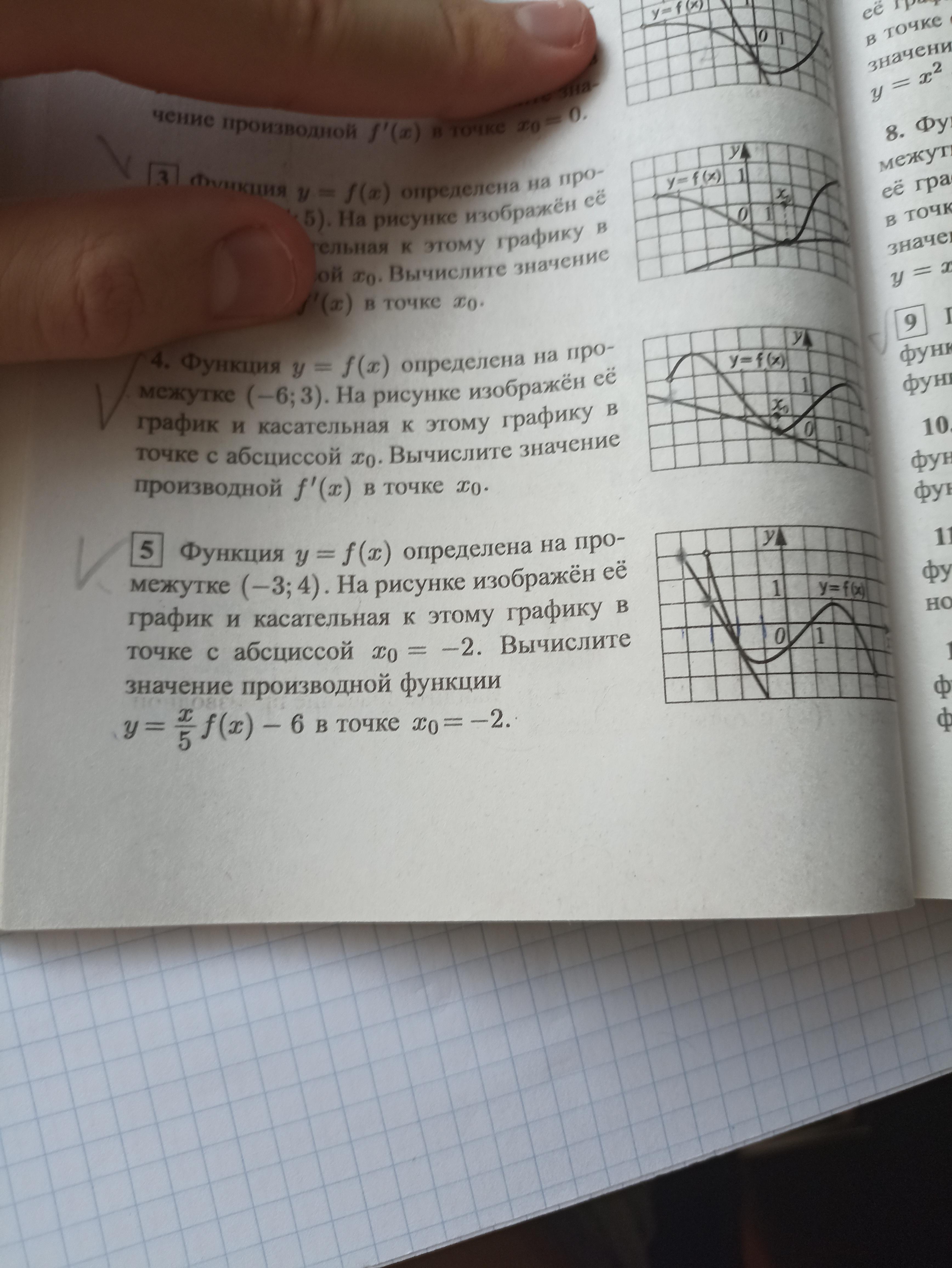
Задание номер 5 помогите решить срочно!!!
Приложения:
Ответы
Автор ответа:
0
Решение .
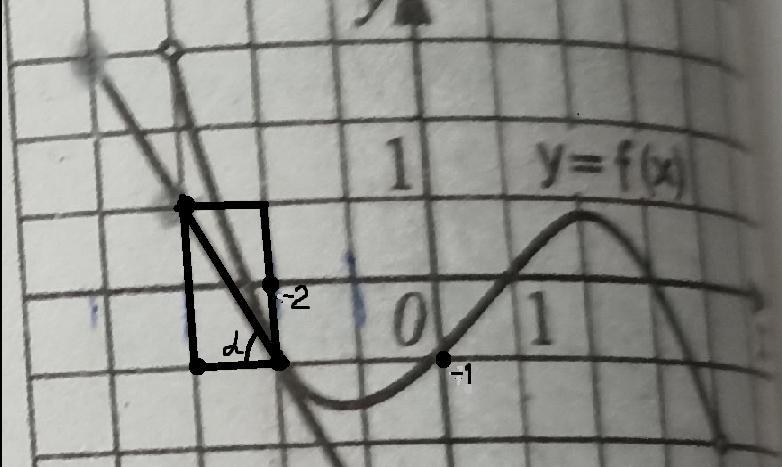
Вычислим значение производной функции y = f(x) в точке x = -2 .
Она равна tgα = - 2/1 = -2 ⇒ f'(-2) = -2 .
Найдём по чертежу значение функции f(x) при х = -2 : f(-2) = -1 .
Поэтому функция при х = -2 имеет производную ,
равную 0 , так как
-
Ответ: .
Приложения:
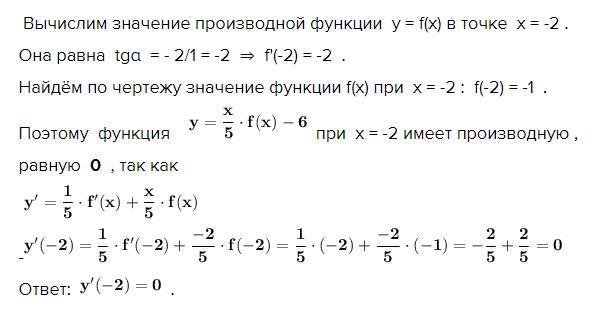
AAAAerfg:
Ответа нет?
есть
Похожие вопросы
Предмет: Қазақ тiлi,
автор: koinvest100
Предмет: Қазақ тiлi,
автор: yasminsuper777
Предмет: Қазақ тiлi,
автор: balgunbekbelekei
Предмет: Английский язык,
автор: avelya2020mic
Предмет: Қазақ тiлi,
автор: Аноним