Предмет: Алгебра,
автор: Hoholololol
ПОМОГИТЕ ППЖПЖПЖПЖПЖПЖПЖПЖПЖПЖ
Приложения:
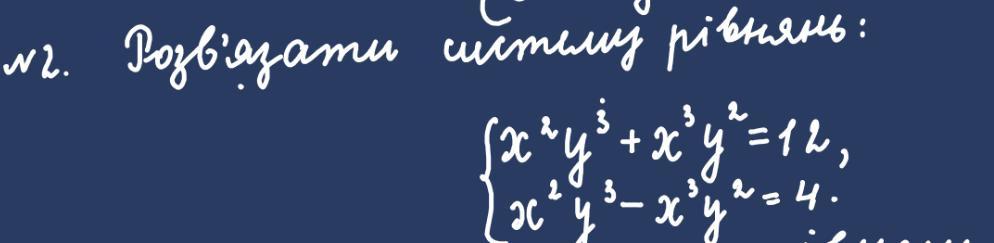
Ответы
Автор ответа:
1
Ответ:
Решить систему уравнений . Сложим первое уравнение со вторым и вычтем .
Приложения:
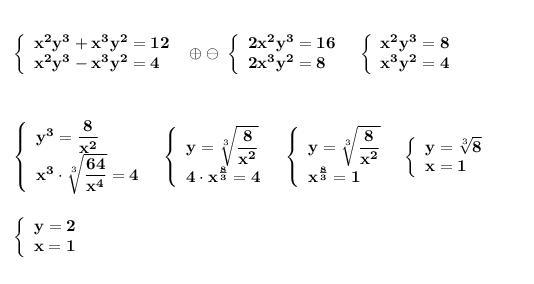
Похожие вопросы
Предмет: Английский язык,
автор: Any0212
Предмет: Українська література,
автор: liashenkoyana2007
Предмет: Литература,
автор: vikasavcuk125
Предмет: История,
автор: arai2019075