Предмет: Геометрия,
автор: Breezly
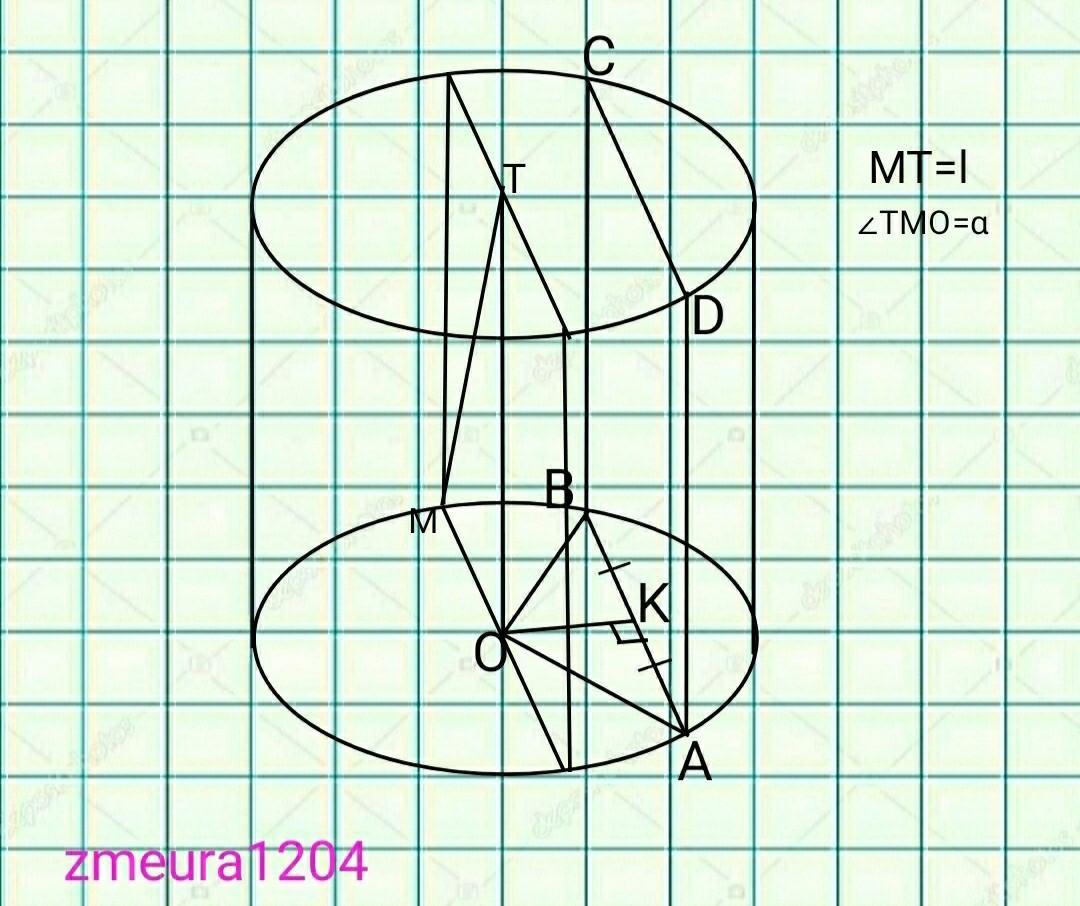
Відрізок, який з’єднує центр верхньої основи прямого циліндра з точкою кола нижньої основи, дорівнює l і нахилений до площини основи під кутом α. Знайдіть: площу осьового перерізу циліндра; відстань між площинами осьового перерізу циліндра і паралельного до нього перерізу, який має вдвічі меншу площу.
Ответы
Автор ответа:
3
Ответ:
1) So.п=l²*sin2α
2) відстань між площинами дорівнює (½*l*cosα*√3)
Объяснение:
∆TMO- прямокутний трикутник.
cos∠TMO=MO/MT; →
MO=MT*cosα=l*cosα - радіус циліндра (R=l*cosα)
sin∠TMO=TO/MT; →
TO=MT*sinα=l*sinα - висота циліндра (Н=l*sinα)
Sо.п.=2R*H=2*l*cosα*l*sinα=l²*sin2α. - площа осьового перерізу циліндра.
So.п.=2*S(ABCD);
S(ABCD)=H*2R/2=HR;
S(ABCD)=H*AB; AB=R.
KA=BK;
AK=R/2=l*cosα/2;.
∆KOA- прямокутний трикутник.
За теоремою Піфагора:
ОК=√(ОА²-АК²)=√(R²-AK²)=
=√((l*cosα)²-(l*cosα/2)²)=
=√(4l²*cos²α/4-l²*cos²α/4)=
=√(3l²*cos²α/4)=½*l*cosα√3; - відстань між площинами осьового перерізу і паралельно до нього перерізу.
Приложения:
zmeura1204:
Можливо десь помилилась.
У вас таке ж завдання, як у cvb.
помогите пожалуйста в профиле вопросы без решения прошу
Похожие вопросы
Предмет: Физика,
автор: rdahsbw
Предмет: Английский язык,
автор: mangos3212
Предмет: Русский язык,
автор: zhumadildanialgg
Предмет: Английский язык,
автор: alinovalim123