Предмет: Геометрия,
автор: hadsonhornet0087
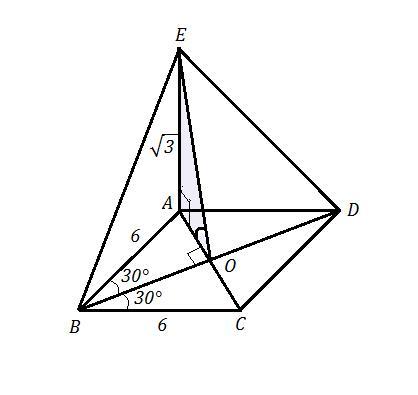
7. Через вершину А ромба ABCD со стороной равной 6м и острым углом в равным 60° провели перпендикуляр АЕ = √3м. Найдите угол наклона плоскости DBE к плоскости треугольника АBC.
amelelilineli:
Ответ нашли?
Ответы
Автор ответа:
2
Ответ:
AВCD - ромб . AB = BC = CD = AD = 6 м , ∠ AВС = 60° ,
АЕ ⊥ ABCD , AE = √3 м
Найти угол наклона пл. DBE к пл. ABC (ABCD) .
АС ∩ BD = O
АBD- диагональ ромба является биссектрисой ∠ АBС ⇒ ∠АВО=30°
Диагонали ромба перпендикулярны : АС ⊥ BD ⇒
Δ АОВ - прямоугольный , ∠АОВ = 90° ⇒
AO = AB · sin30° = 6 · 1/2 = 3 (м)
Угол наклона пл. DBE к пл. ABCD равен ∠AOЕ , так как АО ⊥ BD и
EO ⊥ BD (по теореме о трёх перпендикулярах) ,
∠AOЕ найдём из Δ АОЕ . Так как АЕ ⊥ ABCD , а значит АЕ ⊥ АО , то
∠ЕАО = 90°
tg∠AOЕ = AE / AO = √3 / 3 ⇒ ∠AOE = arctg(√3/3) = 30° .
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: vkhamuda
Предмет: Русский язык,
автор: 2014denchik228
Предмет: Математика,
автор: gkorolev35
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: amindjanovabarno