Здравствуйте, сложные задачи по алгебре, помогите кто нибудь решить задачу пожалуйста , объяснитье если можно, пункт б
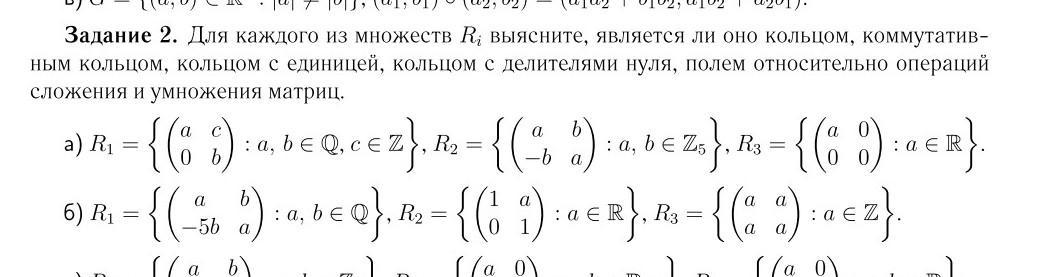
Ответы
Ответ:
Первое множество поле, второе даже незамкнуто относительно умножения, третье - коммутативное кольцо без единицы и без делителей нуля.
Объяснение:
Задание объемное, поэтому придется решать не очень подробно, оставляя детали для подготовленного читателя.
Терминология: кольцо - это абелева группа по сложению (нейтральный элемент 0 называется нулем). Относительно умножения обычно предполагается ассоциативность (то есть это полугруппа); сложение и умножение должны быть связаны двумя дистрибутивными законами (x+y)z=xz+yz; x(y+z)=xy+xz. Поскольку во всех трех заданиях множества являются подмножествами кольца квадратных матриц, ассоциативные, коммутативные и дистрибутивные законы можно не проверять, они выполнены автоматически. Кольцо с единицей - это кольцо, в котором есть нейтральный элемент по умножению e: ex=xe=x для любого x. Если xy=0, но x≠0, y≠0, x и y называются делителями нуля (x - левый делитель, y - правый делитель). Поле - это коммутативное (по умножению, естественно) кольцо с единицей (отличной от нуля), в котором каждый ненулевой элемент обратим (то есть если x≠0, должен существовать y такой, что xy=e). Легко доказать, что в поле нет делителей нуля.
То, что это множество является абелевой группой по сложению, практически очевидно (нулем является нулевая матрица).
Проверим замкнутость множества относительно умножения:
(конечно, мы не забываем посмотреть, откуда берутся числа - в первом задании из поля Q, поэтому операции сложения и умножения не выводят оттуда).
Поскольку ассоциативность и дистрибутивность наследуются, мы имеем кольцо. Поскольку единица кольца всех матриц, то есть матрица принаджежит нашему кольцу, она же будет единицей кольца. Проверив коммутативность умножения (если внимательно посмотреть на результат перемножения выше, коммутативность станет очевидной), видим, что для доказательства того, что это поле, остается проверить только обратимость ненулевых элементов. Пусть A - ненулевая матрица из кольца. То, что AB=e, равносильно системе
Знаменатель отличен от нуля, поскольку раз A ненулевая матрица, или a или b отлично от нуля (или оба). Поскольку с ∈Q, d∈Q, доказано, что обратная матрица для A существует. Итак, в первом примере у нас поле.
Проблемы начинаются с самого начала: сумма двух элементов из этого множества не принадлежит ему! Поэтому это даже не кольцо, даже не группа по сложению.
По сложению проблем не видно (благодаря тому, что Z группа по сложению). По умножению тоже все нормально:
(ведь Z кольцо - произведение целых чисел снова является целым числом).
Итак, у нас кольцо, очевидно коммутативное. А вот нейтрального элемента в нем нет - если AB=A, то Вот если бы коэффициенты брались из поля Q или R, проблем бы не было. Итак, у нас коммутативное кольцо без единицы, поэтому про мечту стать полем оно может забыть. Но хорошо хотя бы то, что в нем нет делителей нуля - ведь если AB=0, то 2ab=0, то есть или a, или b (или оба) =0, то есть одна из этих матриц нулевая.