Здравствуйте, сложные задачи по алгебре, помогите кто нибудь решить задачу пожалуйста , пункт б
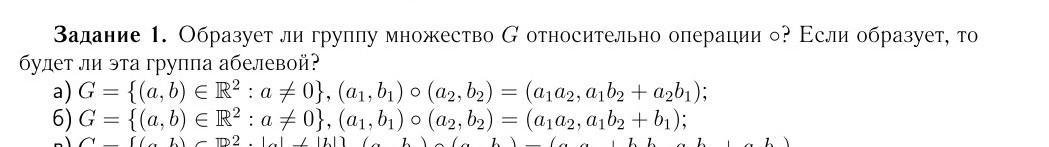
Ответы
Ответ:
Образует неабелеву группу.
Объяснение:
Первое замечание: операция не выводит из G, поскольку если и
то
Проверим сначала коммутатитвность операции (если коммутативность есть, проверка наличия единичного элемента и обратного к каждому элементу упрощается).
Хотя различие результатов перемножения элементов в одном и другом порядке очевидна, можем привести конкретные значения: если то в одном порядке получается пара (2,1), а в другом пара (2,2). Итак, коммутативности нет, поэтому если мы докажем, что G группа, эта группа не будет абелевой.
Проверим ассоциативность операции, то есть что
Левая часть равна
Правая часть равна
Мы видим, что результат получается одинаковый, то есть ассоциативность доказана (то есть доказано, что G полугруппа - если такие термины у Вас в ходу).
Проверим наличие едининого элемента, то есть наличие такой пары что для любой пары
выполнено
Итак, претендент на роль единичного элемента - это
Изменим порядок в произведении:
Итак, мы доказали, что есть единичный элемент (то есть доказано, что G моноид).
Проверим наличие у каждого элемента обратного, то есть что для любой пары можно подобрать пару
такую, что
Изменим порядок в произведении:
Итак, мы доказали, что у каждого элемента есть обратный. Наличие ассоциативности, единичного элемента и обратного элемента означает, что G - группа. Абелевой (то есть коммутативной) она не будет, как мы доказали в самом начале.
Замечание. В процессе рассуждений мы пользовались ассоциативностью обычных операций умножения и сложения в множестве действительных чисел.