Question

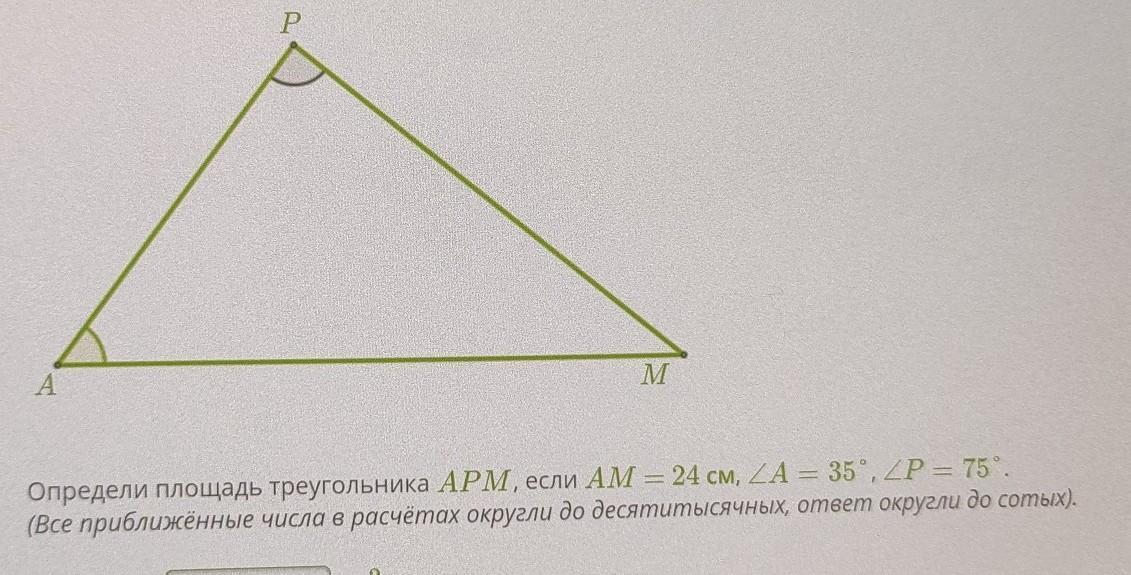
Определи площадь треугольника APM, если АМ = 24 см, ​

Answer 1

Ответ:

Чтобы найти площадь треугольника \(APM\), мы можем использовать формулу для площади треугольника по длинам сторон и углам между ними.

Площадь треугольника можно вычислить по формуле:

\[S = \frac{1}{2} \cdot AB \cdot AC \cdot \sin(\angle A)\]

Где \(AB\) и \(AC\) - длины сторон треугольника, а \(\angle A\) - угол между этими сторонами.

В данном случае \(AB = AM = 24\) см и \(AC = AP\). Мы знаем, что \(\angle A = 35^\circ\). Подставим значения и решим:

\[S = \frac{1}{2} \cdot 24 \cdot AP \cdot \sin(35^\circ)\]

Теперь, чтобы найти длину стороны \(AP\), мы можем использовать закон синусов для треугольника \(APM\):

\[\frac{AP}{\sin(75^\circ)} = \frac{24}{\sin(35^\circ)}\]

Решив это уравнение, найдем значение \(AP\), которое затем можно использовать в формуле для площади треугольника.