Question

Вирішити те що на фото

Answer 1

Відповідь:

2

Пояснення:

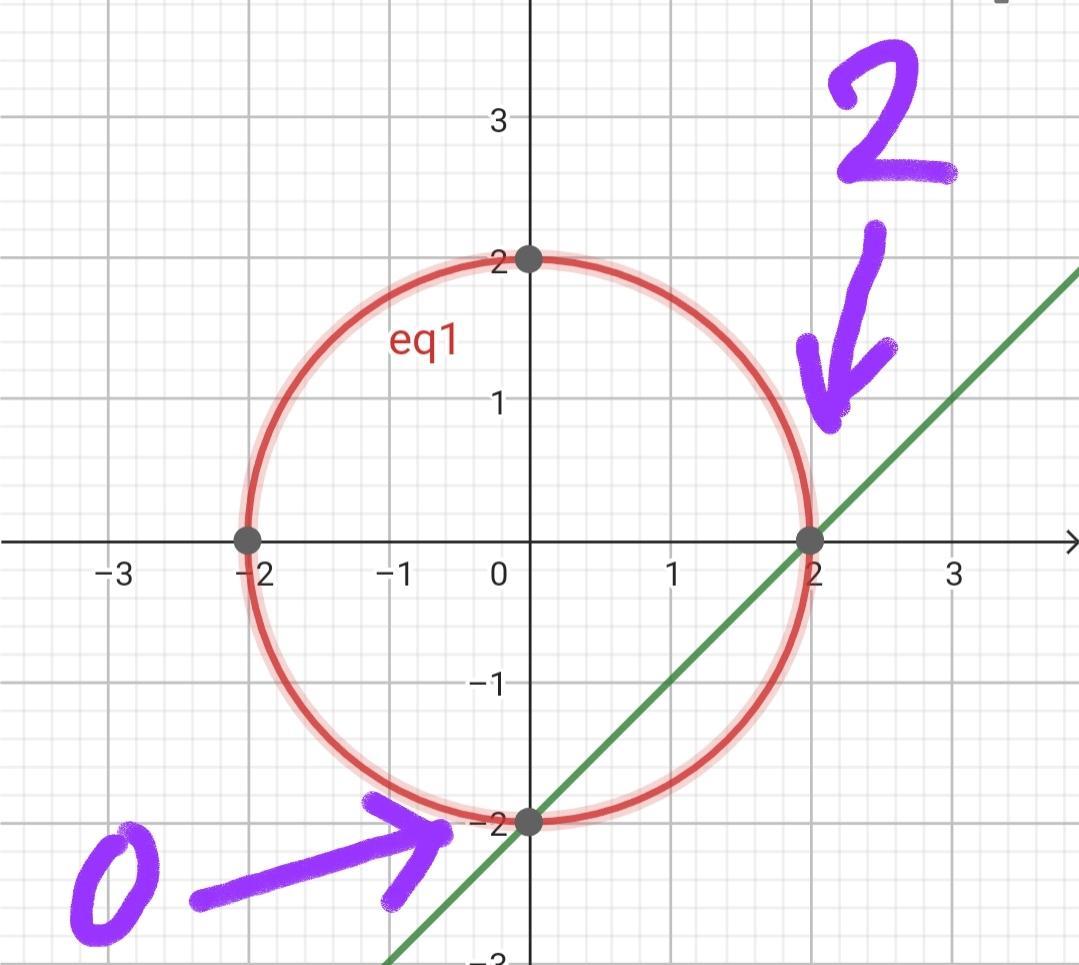
Якщо нам потрібно знайти точки перетину графіків/функцій потрібно їх прирівняти. Знайдемо y із графіка кола:

$x^{2} +y^{2} = 4\\y^{2} =4-x^{2} \\y=\sqrt{4-x^{2} }$

Тепер ми маємо дві функції $y=x-2$ та $y=\sqrt{4-x^{2} }$, прирівнюємо їх:

$x-2=\sqrt{4-x^{2} }$, розвязуємо рівняння. (Спочатку зводимо обидві частини до квадрату):

$(x-2)^{2}=(\sqrt{4-x^{2} })^{2}$ в лівій частині розкриваємо дужки за формулою скороченого множення, а в правій - просто зносимо корінь:

$x^{2} -4x+4=4-x^{2}$

$x^{2} -4x+4-4+x^{2}=0\\2x^{2} -4x=0$ виносимо 2x за дужки:

$2x(x-2)=0$ одже або 2x=0, або x-2=0.

x=0

x=2

нас просять знайти координати перетину, ми знайшли ікси, підставивши їх у любу із двох функцій із умови ми отримаємо ігрики перетину. У нас дві точки, тому нам потрібно записати суму абсцис (абсциса - це ікс), тому ми можемо не шукаючи ігриків просто записати суму іксів. 0+2=2