Предмет: Алгебра,
автор: anonymous789gp
ДОПОМОЖІ БУДЬ ЛАСКА ДАМ 100 БАЛІВ
Приложения:
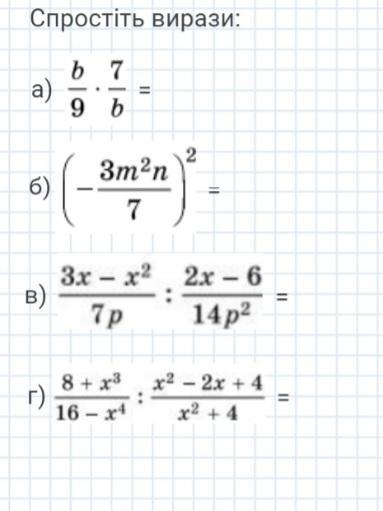
Ответы
Автор ответа:
0
Решение .
Упростить выражения . Применяем формулы сокращённого умножения .
Приложения:


Похожие вопросы
Предмет: Химия,
автор: nalibaevkazbek5
Предмет: Українська мова,
автор: aermolaeva802
Предмет: Литература,
автор: taehyungbutterfly9
Предмет: Математика,
автор: adilesmagambetov78