спростити вираз x^2+5x/(x-5)^2 : (5/x+5 + x^2+25/x^2-25 - 5/5-x
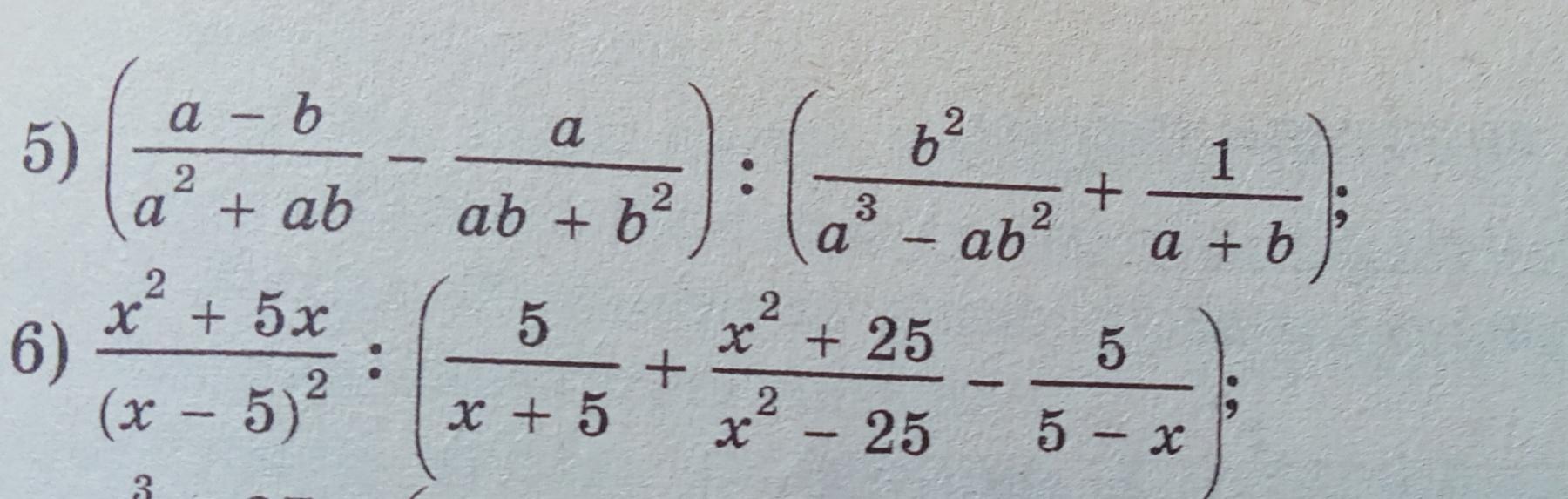
Ответы
Ответ:
Давайте рассмотрим выражение по частям и упростим его:
\( \frac{x^2+5x}{(x-5)^2} : \left( \frac{5}{x+5} + \frac{x^2+25}{x^2-25} - \frac{5}{5-x} \right) \)
Сначала упростим каждое слагаемое внутри скобок.
1. \( \frac{5}{x+5} \) - это уже упрощенное выражение.
2. \( \frac{x^2+25}{x^2-25} \) можно представить как \( \frac{x^2+25}{(x+5)(x-5)} \), это также уже упрощенное выражение.
3. \( \frac{5}{5-x} \) - можно представить как \( \frac{-5}{x-5} \).
Теперь объединим все три слагаемых.
\( \frac{5}{x+5} + \frac{x^2+25}{x^2-25} - \frac{5}{5-x} = \frac{5}{x+5} + \frac{x^2+25}{(x+5)(x-5)} + \frac{-5}{x-5} \)
Теперь объединим исходное выражение.
\( \frac{x^2+5x}{(x-5)^2} : \left( \frac{5}{x+5} + \frac{x^2+25}{x^2-25} - \frac{5}{5-x} \right) = \frac{x^2+5x}{(x-5)^2} : \left( \frac{5}{x+5} + \frac{x^2+25}{(x+5)(x-5)} - \frac{5}{x-5} \right) \)
Теперь найдем общий знаменатель для последнего выражения.
\( \frac{x^2+5x}{(x-5)^2} : \left( \frac{5(x-5)}{(x+5)(x-5)} + \frac{x^2+25}{(x+5)(x-5)} - \frac{5(x+5)}{(x+5)(x-5)} \right) \)
Раскроем скобки.
\( \frac{x^2+5x}{(x-5)^2} : \left( \frac{5x-25+x^2+25-5x-25}{(x+5)(x-5)} \right) \)
Упростим числитель в скобках.
\( \frac{x^2+5x}{(x-5)^2} : \frac{x^2}{(x+5)(x-5)} \)
Теперь упростим деление многочленов.
\( \frac{x^2+5x}{(x-5)^2} \cdot \frac{(x+5)(x-5)}{x^2} \)
Сократим общие члены.
\( \frac{x+5}{x} \)
Объяснение: